第七章：小世界网络模型

第7章 小世界网络模型：
本章将围绕小世界网路模型展开，主要内容分为两个部分：
（1）如何构建具有较大的聚类特性又具有较短的平均距离的小世界网络模型？
（2）什么样的小世界网络才能实现有效搜索？

7.2小世界网络模型

7.2.1小世界网络模型
完全规则最近耦合网络：
高聚类：c=3(k-2)/4(k-1)>=3/8;
平均路径长度：N/2K
完全随机的er图：
没有高聚类：
具有小的平均路径长度：
Cer=K/N-1

于是，规则的最近网络和er随机图都不能再现实际网络同时具有的明显聚类和小世界特征：

然后watts发现：作为从完全规则网络向完全随机网络的过渡：只要在规则网络中引入少许的随机性就可以产生具有小世界特征的网络模型，现在常称为ws小世界模型：

算法7-1 ws小世界模型构造算法
（1）从规则图开始：给定一个含有N个点的环状最近邻耦合网络，其中每个节点都与它左右相邻的各K/2个节点相连，k是偶数
（2）随机化重连：以概率p随机地重新连接网络中原有的每条边，即把每条边的一个端点保持不变，另一个端点改取为网络中随机选择的一个节点。其中规定不得有重边和自环。

[注意]p=1的情形下，算法得到的ws小世界模型与er随机图还是有很大的区别的，因为ws小世界模型中每一个节点的度至少为K/2,而在er随机图中对单个节点的度的最小值没有任何的限制。

7.2.2仿真分析

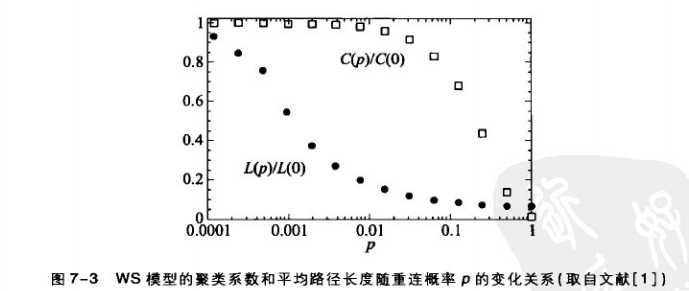
当p开始增大时，随机重连后的网络的聚类系数下降缓慢但平均路径长度下降很快

这意味着，当重连概率p较小时，网络既具有较短的平均长度又具有较高的聚类系数

通过上面的图我们所学到的科学的处理方法：

（1）归一化处理：
（2）对数化坐标：采用对数坐标的好处就是可以在横轴上把较小p值的刻度拉宽较大p值的区间
（3）平均化处理：考虑随机性
从图中我们可以知道：当重连概率p较小时，网络既具有较短的平均路径长度又具有较高的聚类系数。

7.2.3实际验证：
实际的网络有如下的共同特征：La稍大于Lr，但是Ca远大于Cr！

7.2.4动力学分析

ws小世界模型上的病毒传播动力学体现了网络科学研究的一种范式：

（1）建立模型
（2）仿真分析
（3）实际验证
（4）影响分析

在ws模型提出之后，人又提出了另一个在理论分析方面相对容易处理的小世界模型，现在称为nw小世界模型。
算法：
（1）从规则图开始：给定一个含有N个节点的环状最近邻耦合网络，其中每个节点都与它左右相邻的各K/2个节点相连，K是偶数
（2）随机化加边：以概率P在随机选取的Nk/2对节点之间添加边，其中规定不得有重边和自环

总结
小世界模型反映了朋友关系网络的一种特性，即你的大部分朋友都说和你住在同一条街上的邻居或在同一单位工作的同事。另一方面，也有一些人是比较远的，这就是对应ws模型中的重新连边或者nw小世界模型中的随机加边。

7.3 拓扑性质分析

本节主要从理论上分析小世界模型的3个拓扑性质：聚类系数，平均路径长度和度分布

7.3.1聚类系数

1.ws小世界网络

网络中度为Ki的节点i的聚类系数Ci定义为：

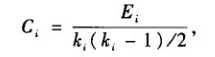
聚类系数的估值为：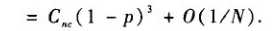

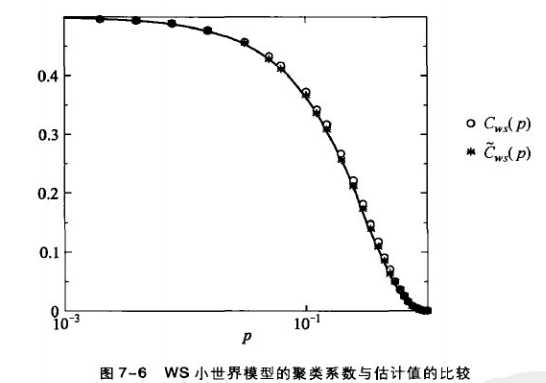
从下图中可以看出聚类系数与p是单调递减的关系，意味着随机性的增强，网络的聚类系数效应减弱。

1.nw小世界网络

（推导太烦了，没看懂）

 7.3.2平均路径长度：

小世界模型的平均长度应该具有如下的形式：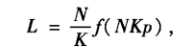

其中F（u）为一与模型参数无关的普适标度函数
经过一系列的推导可得：

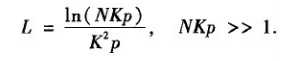
这个式子表名只要网络中随机添加的边数足够多，那么平均路径长度就可以视为网络规模的对数增长函数。

 7.3.3度分布：

1.ws小世界模型的度分布：

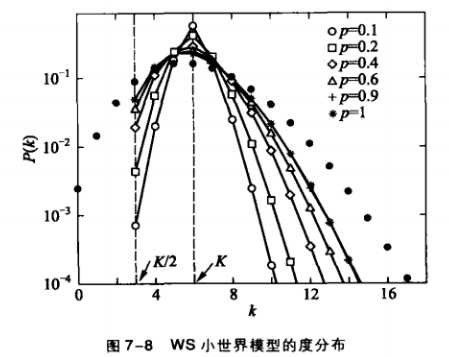
可以看出，p值越大，然后度分布也就越广泛

2.nw小世界模型

当网络中节点数N足够大时，度分布可近似为下面的式子：

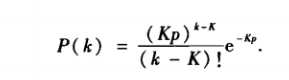
7.4 Kleinberg模型与可搜索性：

尽管连接两个人的路径的数目可能很大，而且不同路径的长度的差异性也可能很大，人们还是可能用简单的分散式算法找到连接自己与陌生人之间的较短的路径。

milgram的小世界实验比较简单，使用的是贪婪算法

但是，一般而言，网络的小世界特性并不意味这网络是可以快速搜索的。如何找到任意两个节点之间的较短的路径依赖于搜索问题的定义，节点提供的网络结构信息，节点使用的搜索算法和整个网络的拓扑结构。

（1）问题定义：随机选择的节点s和t如何考虑最少的步数将信息从s传递带目标节点t。
（2）节点提供的局部信息：当前节点只知道目标节点在网络上的位置和节点之间的局部连接路径。
（3）搜索算法：贪婪算法

由此产生的问题：
什么样的小世界网络是可搜索的， 是否存在最短的平均传递步数的最优网络结构？
为了描述这一问题，将网络模型从一维环状推广到二维网格上。网格中两个节点u v距离为d（u，v）=|k-i|+|l-j。

Kleinberg对二维nw小世界做了如下的修改：

（1）每条边都是有向边
（2）假设长程连接并不是完全随机的添加到原先的规则网络中，节点u有边指向节点v的概率与这两个节点之间的网络距离的幂函数[d（u，v）-阿法]成正比

当a值很大时，添加的边几乎都成为了短程连接。
当a值很小时，添加的边过于随机，几乎就是nw小世界。

是否存在规则性和随机性之间的最佳折中，使得生产的网络即是小世界又便于快速分散式搜索？

最优网络结构

kleinberg进一步从理论上严格证明了 当N->无穷大时，阿法=2是唯一的最优值。

具体的说，对于任意一个给定的阶段，可以将网格中其他节点归于集合Ao，其中Aj包含了所有与节点u的网格距离在区间p[2j，2j+1]内的节点。在a=2时，节点u的每个添加的长程连接的边落在集合Aj中的概率几乎都是相等的，a<2时，添加的连接的另一端点偏向于那些网络距离比较大的集合；当a>2时，添加的连接的另一个端点偏向于那些网格距离比较小的集合。

7.4.3 kleinberg模型的理论分析

 我们需要证明的是当a=1时候，基于局部信息的贪婪算法所需的路径仍然是非常短的。

7.4.4在线网络实验验证

在kleinberg模型中有两个基本假设：

（1）两个节点存在长程连接的概率是由它们之间的网格距离决定的
（我想到一个方向，如果我添加一个“人情因素”是在kleinberg模型基础上添加的是不是使得这样的模型更加的科学呢？）
（2）所有节点在空间上是均匀分布的：
而在实际问题中
（1）短距离中，地理因素占据着主导因素
（2）长距离中，非地理因素占据着主导地位

于是livejournal提出了基于zhi的二维经纬模型：

（我觉得livejournal模型就是基于“人情”的）

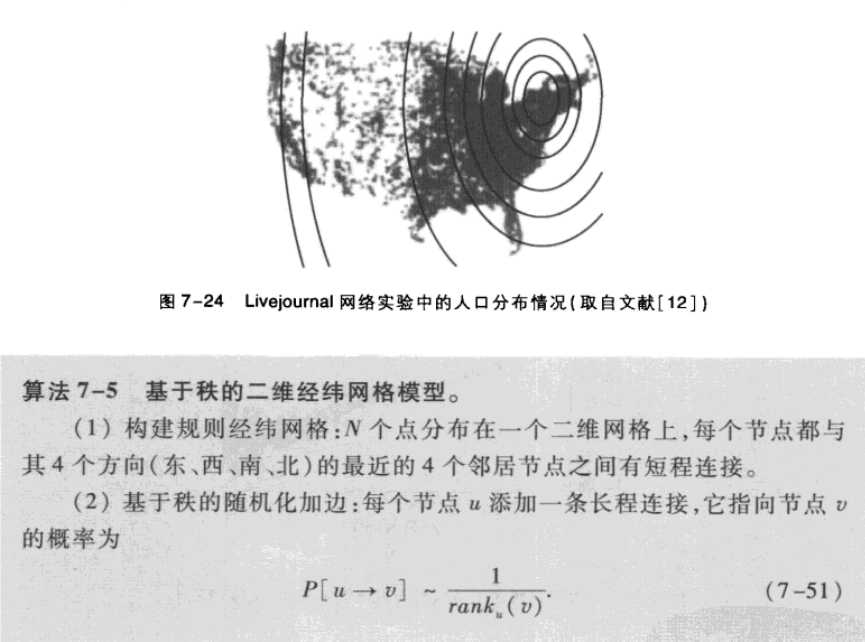
上述研究表明：
（1）从可搜索角度来看，kleinberg仅考虑地理因素对长程连接的影响是合理的，也就是说，在这样的理论模型下是可以找到较短路径的。
（2）从最优化的角度看，基于zhi的模型可能更加的符合实际。