cubic与spline插值点处的区别
cubic与spline都是Matlab的三次样条插值法,但是它们在插值点处仍然有着很微妙的区别,这个区别说明不了两种方法的好坏,只能根据实际情况进行合理筛选。以一维插值为例:
clc
clear
%% load data
load Fig1m
x1=Fig1m(:,1);y1=Fig1m(:,2);
m=x1;n=y1;
m(57)=0.0226;m(83)=0.0326;
m(95)=0.0374;m(97)=0.0378;m(99)=0.0382;
mx=0.0:0.0001:0.065;
ny=interp1(m,n,mx,‘cubic‘); % or ny=interp1(m,n,mx,‘pchip‘);
m1=log(1+mx);n1=ny.*(1+mx);
%% Cubic spline
figure(1)
H=plot(m1,n1,‘-‘,mx,ny,‘-‘,‘LineWidth‘,1.5,‘MarkerSize‘,5);
text(0.005,2.7,‘(a) cubic or pchip‘,‘interpreter‘,‘latex‘,‘fontsize‘,18);
xlabel(‘Strain‘,‘Interpreter‘,‘LaTex‘,‘fontsize‘,18);
ylabel(‘Stress (GPa) ‘,‘interpreter‘,‘latex‘,‘fontsize‘,18);
h=legend(H,‘in1‘,‘in2‘,‘Location‘,‘South‘);
po=get(h,‘Position‘ );
set(h,‘Position‘,[po(1)+0.1, po(2)+0.3, po(3), po(4)]);
h1 = findobj(get(h,‘Children‘),‘String‘,‘in1‘);
set(h1,‘String‘,‘$\sigma_{_E}-\epsilon_{_E}$‘,‘Interpreter‘,‘LaTex‘,‘fontsize‘,15);
h1 = findobj(get(h,‘Children‘),‘String‘,‘in2‘);
set(h1,‘String‘,‘$\sigma_{_E}-\epsilon_{_E}$‘,‘Interpreter‘,‘LaTex‘,‘fontsize‘,15);
h2 = findobj(get(h,‘Children‘),‘String‘,‘in1‘);
set(h2,‘String‘,‘$\sigma-\epsilon$‘,‘Interpreter‘,‘LaTex‘,‘fontsize‘,15);
axis([0 0.08 0 3]);
set(gca,‘xtick‘,0:0.02:0.08,‘ytick‘,0:0.5:3,‘fontsize‘,14);
legend(‘boxoff‘)
Xlim =get(gca,‘xlim‘);
Ylim=get(gca,‘ylim‘);
line([Xlim(1) Xlim(2)],[Ylim(2) Ylim(2)],‘color‘,‘k‘);
line([Xlim(2) Xlim(2)],[Ylim(1) Ylim(2)],‘color‘,‘k‘);
插值效果如下:
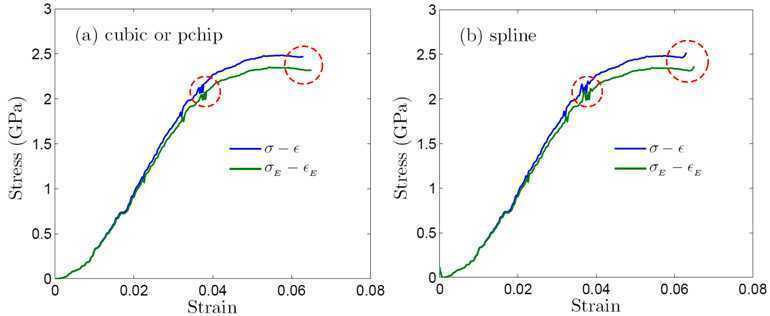
显然,从合理性上看,图(a)是我们所需要的,而图(b)在破浪处浮动过大,更不应该在端点处上挑。这就是说cubic或pchip的插值效果比spline在所给数据的情况下,要更合理一些(b)图须将上述代码做如下局部改变:
ny=interp1(m,n,mx,‘spline‘); % or ny=spline(m,n,mx);
text(0.005,2.7,‘(b) spline‘,‘interpreter‘,‘latex‘,‘fontsize‘,18);
如果,所考虑的数据点是正弦函数的部分数据点,那么样条函数插值后的比较程序可写为:
x=0:10;
y=sin(x);
xi=0:0.25:10;
%将插值方法定义为单元数组
strmod={‘nearest‘, ‘linear‘, ‘spline‘, ‘cubic‘};
%将图标定义为单元数组
str1b={‘(a) method=nearest‘, ‘(b) method=linear‘,...
‘(c) method=spline‘, ‘(d) method=cubic‘};
for i=1:4
yi=interp1(x,y,xi,strmod{i});
subplot(2,2,i)
plot(x,y, ‘ro‘ ,xi,yi, ‘b‘),xlabel(str1b(i))
end
得到的结果如下:
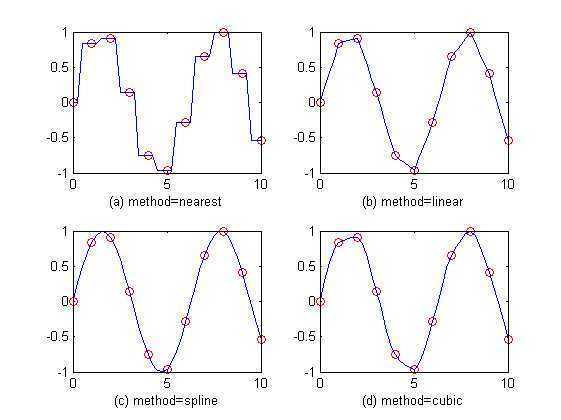
从这幅图中可以看到,spline插值明显比cubic要合理。而其它两种非三次样条插值(临近点插值‘nearest’和线性插值 ‘linear’)的效果均较差。
注:本篇是受新浪2011晓梦蝴蝶的博客的启发写的更为细致的博文,原帖链接:关于MATLAB 插值(Interpolation)。
文章来自:http://www.cnblogs.com/panscience/p/5096631.html