R语言基础
一、扩展包的基本操作语句
R安装好之后,默认自带了"stats" "graphics" "grDevices" "utils" "datasets" "methods"
"base"这七个包,这七个包是不允许被卸载和删除的。
1.扩展包的安装
install.packages("扩展包名称")
2.加载安装包
扩展包安装成功之后,如果要使用其中的功能,需要把它加载到内存中才能使用,默认情况下,R启
动后只加载基本包
library("扩展包名称")或require("扩展包名称")
前者不会返回信息,后者会返回TRUE或FALSE
3.查看已安装的包
Library()
4.查看当前已加载过的包
(.packages())
5.卸载已加载包
detach(package:扩展包名称)
只是卸载,;类似于屏蔽,也就是该包不会被加载使用,而不是删除,是Library的反向操作
6.彻底删除已安装的包
remove. packages("扩展包名称")
7.查看某个包的详细信息
library(help="扩展包名称")
8. 列出安装的包所在的路径
.libPaths()
9.查看扩展包的帮助文档
??扩展包名称
=================================================
二、R的数据结构
R是解释型语言,输入的命令不需要编译或连接等操作,直接就能够被执行。R中所有的操作都是在
内存中进行的,所有能使用的函数都被包含在Library库中,并存放在该名称命名的文件夹下。
1.R的对象和属性
R是通过一些对象来进行的,常见的对象有:
向量、因子、数组、矩阵、数据框、时间序列、列表
所有对象都有两个内在属性:类型和长度
类型是对象元素的基本种类,长度是对象中元素的数目
R的对象元素类型有以下几种
数值型:包括整型、单精度实型、双精度实型
字符型
复数型
逻辑型:FALSE/TRUE、NA
函数或表达式
对象的类型和长度可以通过mode()函数和Length()得到
对于很大的数字可以用指数形式表示:如2.5e20
用Inf和-Inf表示+∞和-∞,用NaN表示不是数字的值
字符型的值在输入时必须加上双引号,如果需要引用双引号,可以让它跟在\后面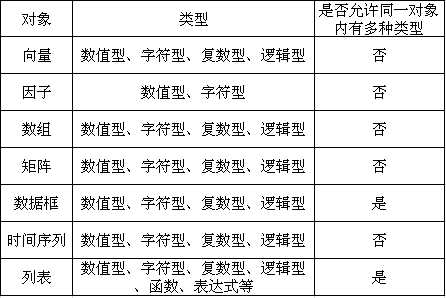
2.向量对象
向量对象是一个变量的取值,是R中最常用最基本的操作对象
最常用的是数值型向量,可以通过以下4种函数建立
seq()或者“:”
rep()
c()
scan()
字符型向量可以通过c()连接,并且可以通过paste()函数进行控制。
逻辑型向量的值可以是TRUE/FALSE、NA
因子型向量不仅包括分类变量自身,也包括变量不同的可能水平,因子利用factor()创建,levels
()用来指定因子的水平,label()用来指定水平的名字,此外函数gl()可以产生规则的因子序列
向量可用于算数表达式,操作是按照向量中的元素一个一个进行的,如果两个向量长度不同,其中
较短向量中的元素会被重复,直到与较长的向量长度相同。
3.数组对象
数组是一个k维的数据表,向量可以看做是k=1的数组,向量、数组、矩阵中的所有元素必须为同一
类型,数组的属性有类型、长度、维度三个。
数组由函数array()建立,共有三个参数
4.矩阵对象
矩阵可以看做是k=2的数组,也可以用array()函数建立,然而,由于矩阵的特殊性,R中更经常使用
matrix()函数来建立矩阵,并且使用diag()函数建立对角矩阵。
5.数据框对象
统计分析中,一个完整的数据集通常是由若干个变量和若干个观测值组成的,这个数据集在R中称为
数据框,数据框在形式上和二维数组类似,并且也有维度这个属性,且各变量的观测值有相同的长
度。和数组不同的是,数据框中行与列的意义是不同的,列表示变量,行表示观测值或个案,R中显
示数据框时,左侧会显示观测值序号。
R中建立数据框分为直接和间接两种方法。
直接法可以使用函数data.frame()直接建立,间接法是指使用函数read.table()读取外部数据文件
。对于矩阵的统计函数,对于数据框也适用,此外,有些关于数据框的其他函数也经常使用,比如
summary():显示主要描述性统计量
pairs():形成散点图
xtables():产生一个列联表
6.时间序列对象
可以使用ts()函数通过一个向量或矩阵创建一个一元或多元时间序列。
7.列表对象
列表对象和数据框类似,最主要的区别是所能包含的元素类型不同,列表可以容纳更为多样化的元
素类型,比如函数或者表达式,这是因为,对于复杂的统计分析,有时某一步的分析结果,需要作
为下一步的参数,这就需要使用列表进行存储。
列表对象可以通过list()函数创建。
=================================================
三、R的数据存储与读取
R对于在文件的读取和写入的工作,使用工作目录来完成,如果一个文件不再工作目录中,则必须给
出他的路径。
1.数据存储
可以使用write.table()或save()函数在文件中写入一个对象或者创建一个文件,也可以使用
write.csv()保存或创建一个逗号分隔的文本文件。
2.数据读取
可以使用函数read.table()、sacn()、read.fwf()
此外,对于excel数据的读取,可以直接复制黏贴或者使用 odbcConnectExcel()函数,前提是安装
了RODBC包。
=================================================
四、R软件编程
1.控制结构
(1)条件语句
if(条件) 表达式1 else 表达式2
ifelse(条件,yes,no)
(2)循环
for(变量 in 变量)表达式
while(条件) 表达式
两种循环略有区别:如果知道终止条件,则用for,如果无法知道循环次数,则用while
通常将一组命令放在{}内
2.向量化
所谓向量化,就是指用向量的形式代替某些循环和控制结构,这样做有很多好处:
可以使代码更简洁,同时也极大提高了运行效率。
3.编写一个函数应该尽量指明返回值,一般用return()函数给出返回值,函数在内部处理过程中,
一般遇到return()函数,就会终止运行,将return()内的数据作为函数处理的结果输出。
=================================================
五、R的图形绘制
1.R中的两种绘图函数
(1)高级绘图函数,用来创建一个新的图形
(2)低级绘图函数,在已存在的图形上添加元素
2.绘图参数
图形的显示可以用绘图参数进行改良,绘图参数可以作为图形函数的选项,也可以使用函数par()永
久的改变绘图参数。
3.常用的图形及函数
(1)直方图:hist()
(2)散点图:plot()
(3)折线图:matplot()
(4)箱线图:boxplot()
(5)饼图:pie()
(6)条形图:barplot()
=================================================
六、描述性统计
1.几种常见分布
(1)正态分布
属于对称分布,其均值、中位数、众数均相等,主要性质有
·图像由其均值和方差完全描述
·函数图像关于均值左右对称,随机变量落在均值两边的概率相等,偏度为0,峰度为3
·两个正态分布的随机变量经过线性组合得到的新随机变量仍然服从正态分布
均值为0,方差为1的正态分布称为标准正态分布。
使用curve(dnor())创建图像
(2)对数正态分布
·随机变量的自然对数服从的正态分布
·取值范围大于等于0
·函数图像右偏
使用curve(dlnorm())创建图像
(3)t分布
与正态分布类似,也属于对称分布
·图像由其自由度完全描述
·随着自由度增加,t分布越来越接近标准正态分布
使用curve(dt())创建图像
(4)卡方分布
若n个相互独立的随机变量服从标准正态分布,那么这n个随机变量的平方和构成的新的随机变量服
从自由度为n的卡方分布。
·图像由其自由度完全描述
·取值范围大于等于0
·函数图像右偏
使用curve(dchisq())创建图像
(5)F分布
两个相互独立的随机变量分别服从自由度为m和n的卡方分布,他们相除之后产生的新的随机变量服
从自由度为(m,n)的F分布
·图像由两个自由度完全描述
·取值范围大于等于0
·函数图像右偏
使用curve(df())创建图像
2.连续变量的统计描述
(1)数据集中程度的常用描述统计量
常用五数分别为最大值、最小值、四分位低值、四分位高值、中位数
可以使用fivenum()函数可以一次性返回该五个数字,但是只是五个数字的排列,没有标识,顺序为
最小值、四分位低值、中位数、四分位高值、最大值。
此外,还可以通过单独的函数,返回单个数值
quantile()返回四分位数
median()返回中位数
max()返回最大值
min()返回最小值
mean()返回均值
还有一个函数是summary(),结果返回五数和均值
(2)数据离散程度的常用描述统计量
IQR()返回四分位极差,也就是四分位高值-四分位低值
sd()返回标准差
var()返回方差
mad()返回绝对离差
kurtosis()返回峰度
skewness()返回偏度
R的基本包没有包含峰度和偏度这两个函数,需要加载扩展包fBasics
(3)实例应用
单列数据:
> setwd(choose.dir()) #首先选择工作目录,可以将文件所在的目录设为工作目录,choose.dir
()函数会弹出选择窗口,可以直接选择而不要手动输入绝对路径
> library(RODBC) #先加载RODBC包
> z<- odbcConnectExcel(basename(choose.files())) #也可以直接使用绝对路径,但是由于R使
用的是正斜杠,而一般路径都是反斜杠,需要转换比较麻烦,因此我们使用choose.files()函数直
接选择文件,并用basename()函数直接提取文件名
> sq<-sqlFetch(z,"Sheet1") #从一个ODBC中读取表格到数据框中
> summary(sq$consumption) #返回五数和均值,sq$consumption为根据变量名选择数据框中的某列
,下同,注意必须是数据框
> mean(sq$consumption) #返回均值
> fivenum(sq$consumption) #返回五数
> median(sq$consumption) #返回中位数
> max(sq$consumption) #返回最大值
> min(sq$consumption) #返回最小值
> IQR(sq$consumption) #返回四分位极差
> sd(sq$consumption) #返回标准差
> var(sq$consumption) #返回方差
> mad(sq$consumption) #返回绝对离差
******************************************
多列数据
在此我们使用基本包datasets中的state.x77中的数据为例,该数据是一个多列数据
> m<- data.frame(state.x77) #先将数据加入到数据框中,这样才可以根据变量名选择某列
> summary(m) #summary()函数可以直接对多列数据进行处理,返回的结果以列的形式分组
> max(m) #max等函数只能处理单列数据,如果直接以整个数据框为参数的话,会把所有列的数据合
并成一列再进行计算,不会按每列进行,因此我们需要先将数据加入数据框中,根据变量名选择列
进行计算。
> max(m$Frost)
> aggregate(state.x77,list(region=state.region,cold=state.x77[,"Frost"]>130),mean)
#可以使用aggregate()函数进行有条件的分组计算,其中第一个参数为数据框,第二个参数为分组
条件,第三个参数为统计函数,注意第二个条件中筛选出的数据框大小要和第一个参数的数据大小
一致,否则会报错。
> var(state.x77) #计算方差协方差矩阵
3.分类变量的统计描述
如果变量为分类变量,那么对应的数据为分类数据,是属于离散型的数据,此类数据一般都是统计
其频数,常使用表格来描述。
(1)频数列联表
对于二维的列联表,可以使用矩阵进行建立
举例:
> eye.hair<-matrix(c(68,20,15,5,119,84,54,29,26,17,14,14,7,94,10,16),nrow=4,byrow=T)
#byrow参数为逻辑值,如果是默认值False,则为按列填充,否则为按行填充,本例为按行填充
> colnames(eye.hair)<-c("brown","blue","hazel","green") #为矩阵设置列名
> rownames(eye.hair)<-c("black","brown","red","blond") #为矩阵设置行名
> eye.hair
(2)获得列联表的边际值
也就是矩阵行或列的求和,可使用margin.table()函数
> margin.table(eye.hair,1) #按列相加
> margin.table(eye.hair,2) #按行相加
(3)相对频数列联表
列联表中的频数除以边际值,就可以得到相对频数列联表,再乘以100,就可以得到百分比相对频数
列联表。可以通过prop.table()函数得到
> prop.table(eye.hair,1) #按列相对频数
> prop.table(eye.hair,2) #按行相对频数
> eye.hair/sum(eye.hair) #全局相对频数
(4)图形描述
我们使用R自带的数据集HairEyeColor,首先创建条形图
> a<-apply(HairEyeColor,c(1,2),sum) #由于数据集是按照性别区分成两个列联表,我们需要使用
apply函数对这两个表进行加总,c(1,2)表示按照行和列处理
> barplot(a)
还可以使用dotchart()函数创建Cleveland点图
> dotchart(a)
=================================================
七、参数估计与样本量估计
1.单正态总体均值区间估计
(1)方差已知时
R中没有现成的方差已知时的求均值置信区间的函数,需要自己编写
> aaa <- function (x,a,b) {
+ n<-length(x)
+ mean<-mean(x)
+ result<-c(mean-a*qnorm(1-b/2)/sqrt(n),mean+a*qnorm(1-b/2)/sqrt(n))
+ result
+
+ }
举例:某产品重量服从正态分布N(μ,0.6),现抽取6个,测得重量为:
14.6,15.1,14.9,14.8,15.2,15.1
请求平均重量置信度为95%的置信区间
> x<-c(14.6,15.1,14.9,14.8,15.2,15.1)
> a<-sqrt(0.6)
> aaa(x,a,0.05)
[1] 14.3302 15.5698
(2)方差未知时
方差未知时,可以直接使用t.test()函数
举例:某产品重量服从正态分布N(μ,σ方),σ未知,现抽取9个,测得重量为:
99.3,98.7,100.5,101.2,98.3,99.7,99.5,102.1,100.5
请求平均重量置信度为95%的置信区间
> x<-c(99.3,98.7,100.5,101.2,98.3,99.7,99.5,102.1,100.5)
> t.test(x)
One Sample t-test
data: x
t = 247.43, df = 8, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
99.04599 100.90956
sample estimates:
mean of x
99.97778
结果很多,我们可以只提取想要的
> t.test(x)$conf
2.单正态总体方差区间估计
(1)均值未知时
虽然也可以分为均值已知和均值未知两种情况,但是实际中均值已知的情形极为罕见,因此不再讨
论该情况。
R中没有求方差置信区间的函数,因此需要自己编写函数
> bbb<-function(n,s2,a){
+ result<-c((n-1)*s2/qchisq(a/2,df=n-1,lower.tail=F),
+ (n-1)*s2/qchisq(1-a/2,df=n-1,lower.tail=F))
+ result
+ }
举例:抽取某产品16件,测得平均长度为12.8,方差为0.0023,假设零件长度服从正态分布,请求
总体方差和标准差的置信度为95%的置信区间。
3.双正态总体均值差区间估计
(1)两方差已知时
R中没有求两方差已知时两均值差的置信区间函数,需要自己编写函数
> two<-function(x,y,z,a,b){
+ options(digits = 4)
+ m=length(x);n=length(y)
+ xbar=mean(x)-mean(y)
+ alpha=1-z
+ zstar=qnorm(1-alpha/2)*(a/m+b/n)^(1/2)
+ xbar+c(-zstar,+zstar)
+ }
举例:为比较两种产品的产量,选取18块类似的试验田,采用相同的耕作方式,产量如下
甲品种:628,583,510,554,612,523,530,615
乙品种:535,433,398,470,567,480,498,560,503,426
假设产量服从正态分布,甲品种方差2140,乙品种方差3250,请求两个品种平均产量差的置信度为
95%的置信区间> x<-c(628,583,510,554,612,523,530,615)
> y<-c(535,433,398,470,567,480,498,560,503,426)
> a=2140
> b=3250
> z=0.95
> two(x,y,z,a,b)
[1] 34.67 130.08
(2)辆房车未知但相等时
两方差未知但是相等,可以使用t.test()函数,只需将参数var.equal=TRUE即可
> x<-c(628,583,510,554,612,523,530,615)
> y<-c(535,433,398,470,567,480,498,560,503,426)
> t.test(x,y,var.equal = TRUE)
4.双正态总体方差比区间估计
和单正态总体方差区间估计一样,只讨论均值未知的情况,R中提供了内置函数var.test()求方差比
的置信区间。
举例:甲乙两种产品重量服从正态分布,现分别抽取若干,测得重量如下
甲:20.5,19.8,19.7,20.4,20.1,20,19,19.9
乙:20.7,19.8,19.5,20.8,20.4,19.6,20.2
请求出甲乙两产品方差比0.95的置信区间
> b<-c(20.7,19.8,19.5,20.8,20.4,19.6,20.2)
> a<-c(20.5,19.8,19.7,20.4,20.1,20,19,19.9)
> var.test(a,b)
5.确定样本容量
(1)总体方差已知情况下,估计均值时样本容量的确定
R中没有求此类问题的函数,需要自己编写
> size1<-function(a,b,c){
+ alpha=1-c
+ ((qnorm(1-alpha/2)*b^(1/2))/a)^2
+ }
举例:某地区10000户,现想抽取一部分调查,要求置信度为95%,最大允许误差为2,根据经验,方
差为500,求应抽取多少户做调查。
> size1(2,500,0.95)
[1] 480.1824
(2)总体方差未知情况下,估计均值时样本容量的确定
R中没有求此类问题的函数,需要自己编写,注意函数中使用了while循环,
> size2<-function(a,b,c,d){
+ t1<-qt(b/2,d,lower.tail = FALSE)
+ n1<-(t1*a/c)^2
+ t2<-qt(b/2,n1,lower.tail = FALSE)
+ n2<-(t2*a/c)^2
+ while(abs(n2-n1)>0.5){
+ n1<-(qt(b/2,n2,lower.tail = FALSE)*a/c)^2
+ n2<-(qt(b/2,n1,lower.tail = FALSE)*a/c)^2
+ }
+ n2
+ }
举例:某公司生产一批产品,重量服从正态分布,现在要估计这批产品的平均重量,最大允许误差
为2,样本标准差为10,请问在0.01置信度下应抽取多少样本
> size2(10,0.01,2,100)
[1] 169.6658
(3)估计比例P时样本容量的确定
此问题设计p的取值,可以根据经验能给出p的估计值或取值范围,取值范围包括0.5时,取0.5,如
果不包括0.5,则取接近0.5的值,如果没有任何先验经验,则p取0.5
R中没有求此类问题的函数,需要自己编写
> size3<-function(a,p,c){
+ alpha=1-c
+ ((qnorm(1-alpha/2))/a)^2*p*(1-p)
+ }
举例:某大学历届毕业生就业率为90%,现要估计本届毕业生的就业率,要求服从不超过3%,置信水
平为0.05,要抽取多少样本?
> size3(0.03,0.9,0.95)
[1] 384.1459
=================================================
八、参数假设检验
原假设是有怀疑,想要拒绝的假设,记为H0,备择假设是拒绝原假设之后得到的结论,记为H1,无
论是单尾检验还是双尾检验,等号永远在原假设这一边。
允许犯第一类错误的概率为显著性水平
1.单样本t检验
例题:某公司业务员人均月销量为500,现采取新的广告策略,一段时间后抽取20名业务员统计人均
月销量,问广告策略能否影响销量?显著性水平为0.05
> setwd(choose.dir())
> library(RODBC)
> z<-odbcConnectExcel(basename(choose.files()))
> sq<-sqlFetch(z,"Sheet1")
> t.test(sq$sale,mu=500,conf.level = 0.95)
原假设为广告不能影响销量
备注假设为广告可以影响销量
R中可以直接使用t.test()函数进行t检验,结果显示p值大于0.05,不能拒绝原假设。
2.两独立样本t检验
两独立样本t检验分为方差相等和不等两种情况。为此需要先做方差的差异性检验,可以使用
var.test()函数
举例:有两个基金公司各管理40支基金,试分析两公司基金价格之间有无差异,显著性水平为0.05
> setwd(choose.dir())
> library(RODBC)
> z<-odbcConnectExcel(basename(choose.files()))
> sq<-sqlFetch(z,"Sheet1")
> var.test(sq$fa,sq$fb)
结果显示p-value=0.0015,可认为方差不等,接下来使用t.test()函数
> t.test(sq$fa,sq$fb,var.equal = FALSE,paired = FALSE),将var.equal = FALSE设置即可。如
果方差相等,设为TRUE。
结果p-value < 2.2e-16,拒绝原假设,认为二者存在差异。
3.配对样本t检验
与独立样本t检验的区别是:两个样本来自同一总体,且数据顺序不能调换
举例:为研究一种政策效果,抽取了50支股票进行实验,记录实施政策前后的价格,试分析政策是
否能引起股票价格的变化,显著性水平为0.05
> setwd(choose.dir())
> library(RODBC)
> z<-odbcConnectExcel(basename(choose.files()))
> sq<-sqlFetch(z,"Sheet1")
> t.test(sq$qian,sq$hou,paired = TRUE)
将paired参数设置为TRUE,结果p-value < 2.2e-16,小于0.05,拒绝原假设,认为政策引起了股票
价格的变化。
4.单样本方差检验
R中没有做单样本方差检验的内置函数,需要自己编写
> chisq.var.test<-function(x,var,a){
+ n<-length(x)
+ s2<-var(x)
+ chi2<-(n-1)*s2/var
+ p<-pchisq(chi2,n-1)
+ p.value<-p
+ p.value
+ }
举例:抽取某产品50个,测得重量,分析其方差是否等于1,显著性水平为0.05
> setwd(choose.dir())
> library(RODBC)
> z<-odbcConnectExcel(basename(choose.files()))
> sq<-sqlFetch(z,"Sheet1")
> chisq.var.test(sq$syl,1,0.05)
[1] 2.194693e-09
从结果中看出,p值远小于0.05,拒绝原假设,可认为方差不等于1
5.双样本方差检验
可以使用var.test()函数完成
举例:为研究两只基金收益波动情况是否相同,现抽取这两只基金20天的收益情况,试分析其方差
是否相同,显著性水平为0.05
> setwd(choose.dir())
> library(RODBC)
> z<-odbcConnectExcel(basename(choose.files()))
> sq<-sqlFetch(z,"Sheet1")
> var.test(sq$returnA,sq$returnB)
结果p-value = 0.953 不能拒绝原价,也就是说这两只基金波动情况相同。
=================================================
九、相关分析与回归分析
1.相关分析
可以使用cor()函数和cov()函数计算相关系数和协方差
举例:现在想分析广告费和销售额之间的关系,收集了12个月的数据
> setwd(choose.dir())
> library(RODBC)
> z<-odbcConnectExcel(basename(choose.files()))
> sq<-sqlFetch(z,"Sheet1")
> cor(sq)
time adv sale
time 1.0000000 0.9773278 0.9797958
adv 0.9773278 1.0000000 0.9636817
sale 0.9797958 0.9636817 1.0000000
> cov(sq)
time adv sale
time 13.0000 286.9545 352.1364
adv 286.9545 6631.3561 7822.3712
sale 352.1364 7822.3712 9935.9015
上述输出的是相关系数矩阵和协方差矩阵,事实上,time并不需要参加分析,因此我们也可以只指
定想要分析的变量
> cor(sq$adv,sq$sale)
[1] 0.9636817
也可以将需要分析的变量加入一个数据框中再分析
> bb<-data.frame(sq$adv,sq$sale)
> cor(bb)
sq.adv sq.sale
sq.adv 1.0000000 0.9636817
sq.sale 0.9636817 1.0000000
2.一元线性回归分析
举例:为研究销售人员数量与销售额之间的关系,收集了一些数据,请用简单线性回归分析销售人
员数量对销售额的影响。
#打开数据文件,excel表格
setwd(choose.dir())
library(RODBC)
z<-odbcConnectExcel(basename(choose.files()))
sq<-sqlFetch(z,"Sheet1")
#对变量进行描述性分析和相关性分析
> summary(data.frame(sq$xse,sq$rs))
> cor(sq$xse,sq$rs)
#进行回归分析,1表示带有截距,+sq$rs表示含有该自变量
> lm.reg<-lm(sq$xse~1+sq$rs)
#查看回归结果
> lm.reg
Call:
lm(formula = sq$xse ~ 1 + sq$rs)
Coefficients:
(Intercept) sq$rs
176.30 12.23
基本的只显示回归系数,如果想要看汇总的结果,可以使用summary()函数
> summary(lm.reg)
如果想查看lm.reg结果中的某项,也可以使用选择变量的形式,如:
> lm.reg$residuals 查看残差
> lm.reg$coefficients 查看系数
#求置信区间
> confint(lm.reg)
2.5 % 97.5 %
(Intercept) 113.279335 239.31107
sq$rs 9.727714 14.73426
#进行预测
若求re=40时置信水平为0.95的预测值和预测区间,可用predict()函数
3.多元线性回归
举例:收集了四个自变量和一个因变量,试分析他们之间的关系
#打开数据文件,excel表格
setwd(choose.dir())
library(RODBC)
z<-odbcConnectExcel(basename(choose.files()))
sq<-sqlFetch(z,"Sheet1")
#对变量进行描述性分析和相关性分析,由于变量较多,因此我们进行预定义
> y<-sq$TC;x1<-sq$Q;x2<-sq$PL;x3<-sq$PF;x4<-sq$PK
> d<-data.frame(y,x1,x2,x3,x4)
> summary(d)
> cor(d)
#进行回归分析,1表示带有截距
> lm.reg<-lm(y~1+x1+x2+x3+x4)
#查看回归结果
> summary(lm.reg)
结果显示x4不显著,剔除之后再做回归分析
> lm.reg<-lm(y~1+x1+x2+x3)
> summary(lm.reg)
4.多重共线性的诊断
多重共线性是指自变量之间存在线性关系,此问题会导致参数估计的误差增大,多重共线性的诊断
主要有以下几种方法
(1)特征值法
(2)条件指数法
(3)方差膨胀因子法(VIF)
出现多重共线性时,可以使用逐步回归法解决,R中提供了step()函数实现,格式如下
> step(object,scope,direction,...)
其中,object是线性模型或广义线性模型分析的结果,scope用于确定逐步搜索的区域,direction
确定逐步搜索的方向,默认为both,也就是逐步回归,backword为向后法,forword为向前法。
> step(lm.reg)
5.自相关
自相关可以使用残差图和DW检验进行判断。
6.异方差问题
可以使用残差图或加权最小二乘法处理
7.广义线性回归模型
R中使用glm()来拟合广义线性回归模型,格式如下
glm(formula,family=family.generator,data=data.frame)
其中,formula为拟合公式,其意义与线性模型相同,family为分布簇,同时可以通过选项link=来
指定使用的连接函数吗,data为数据框。
(1)基于正态分布:glm(formula,family=gaossian(link=identity),data=data.frame)
(2)基于二项分布:glm(formula,family=binomial(link=logit),data=data.frame)
(3)基于泊松分布:glm(formula,family=poisson(link=log),data=data.frame)
(4)基于伽马分布:glm(formula,family=gama(link=inverse),data=data.frame)
默认值为基于正态分布簇,正态分布簇的广义线性模型等同于一般线性模型。
举例:对45名驾驶员的调查结果,试分析Z1,Z2,Z3与W的关系
#打开数据文件,excel表格
setwd(choose.dir())
library(RODBC)
z<-odbcConnectExcel(basename(choose.files()))
sq<-sqlFetch(z,"Sheet1")
#预定义自变量和数据框
> x1<-sq$z1;x2<-sq$z2;x3<-sq$z3;y<-sq$w
> acc<-data.frame(x1,x2,x3,y)
#进行逻辑回归
> log<-glm(y~x1+x2+x3,family = binomial(link = logit),data = acc)
> summary(log)
8.稳健回归
当存在离群值或高杠杆点时,普通最小二乘法会受此影响,此时应采用稳健回归,其在估计回归参
数时,根据观测值的稳健情况对观测值进行权重赋值,因此稳健回归也属于加权最小二乘回归。
R中的MASS包的rlm函数提供了基于Huber、hampel、bisquare的稳健估计。
举例:我们使用foreign包的crime数据集
#打开数据集并使用普通最小二乘法拟合,作图观察残差、拟合值、Cook距离和杠杆率
> library(foreign)
> cdata<-read.dta("http://www.ats.ucla.edu/stat/data/crime.dta")
> ols<-lm(crime~poverty+single,data = cdata)
> summary(ols)
> opar<-par(mfrow=c(2,2),oma=c(0,0,1.1,0))
> plot(ols,las=1)
从图中可以看出,9、25、51号观测值可能是离群点,我们从数据集中把他们提取出来
> cdata[c(9,25,51),1:2]
接下来观察cook距离较大的观测值,在判断cook距离大小的时候,通常采用的经验分界点是cook距
离序列的4/n处,其中n是观测值个数。
> library(MASS)
> d1<-cooks.distance(ols)
> r<-stdres(ols)
> a<-cbind(cdata,d1,r)
> a[d1>4/51,]
接下来生成一个变量,其对应的为残差序列的绝对值,取出残差绝对值较大的前十个观测值
> rabs<-abs(r)
> a<-cbind(cdata,d1,r,rabs)
> asorted<-a[order(-rabs),]
> asorted[1:10]
> asorted[1:10,]
接下来使用huber方法进行稳健回归估计,并提取残差绝对值和相应的赋予的权重
> huber<-rlm(crime~poverty+single,data = cdata,psi=psi.huber)
> hweights<-data.frame(state=cdata$state,resid=huber$residuals,weight=huber$w)
> hweights2<-hweights[order(huber$w),]
> hweights2
从结果中可以看出,观测值的残差绝对值越大,被赋予的权重越小,而很多观测值被赋予权重为1,
在普通最小二乘法中,所有观测值的权重都为1,因此稳健回归中权重为1的观测值越多。其结果与
普通最小二乘法回归的结果越接近。
接下来使用bisquare法进行稳健回归估计,同样提取残差绝对值和相应的赋予的权重
> bisquare<-rlm(crime~poverty+single,data = cdata,psi = psi.bisquare)
> bweights<-data.frame(state=cdata$state,resid=bisquare$residuals,weight=bisquare$w)
> bweights2<-bweights[order(bisquare$w),]
> bweights2
从结果中可见,两种方法的残差和权重不太一样,但都是残差绝对值越大,赋予的权重越小。
huber方法的缺点在于无法很好的处理极端离群点,而bisquare方法的缺点在于回归结果不容易收敛
,以至于经常有多个最优解。
当稳健回归和普通最小二乘回归的结果差异很大时,通常暗示离群点对于模型参数产生了较大影响
,此时采用稳健回归较为妥当。
=================================================
十.主成分分析和因子分析
1.主成分分析
求原始指标的主成分,也就是求出原始指标的协方差矩阵的特征根及相应的标准化正交特征向量
(1)主成分分析能消除指标间相关关系的影响,减少了指标选择的工作量
(2)主成分分析所得的指标系数和协方差贡献率是从协方差矩阵中得到的,具有客观性
(3)由于同一评价对象在不同样本集合中的均值和离散程度不一样,协方差矩阵也不一样。因此综
合评价结果不稳定,同一被评价对象在不同样本间的评价结果不具有可比性。但是随着样本量的增
大,均值和离散程度将趋于稳定,因此主成分分析适合于大样本容量的情况下。
举例:收集了30个个案的4个指标数据,使用主成分对其分析
#打开数据集
> setwd(choose.dir())
> library(RODBC)
> z<-odbcConnectExcel(basename(choose.files()))
> sq<-sqlFetch(z,"Sheet1")
#接下来进行主成分分析,先定义数据框,因为主成分分析函数princomp需要以数据框形式引入数据
> d<-data.frame(v1=sq$X1,v2=sq$X2,v3=sq$X3,v4=sq$X4)
> pr=princomp(d,cor = TRUE)
> summary(pr,loadings = TRUE)
此处的loading的作用是列出主成分对应原始变量的系数也就是载荷
2.因子分析
因子分析是研究相关矩阵内部依存关系,将多个变量综合为少数几个因子以实现指标与因子之间相
关关系的一种统计方法。
因此,一个完全的因子解应包括因子模型和因子结构两个方面,因子结构即通过相关系数来反映指
标与因子之间的相关关系,因子模型是以回归方程的形式将指标表示为因子的线性组合。
因子分析的基本问题之一,就是估计因子载荷矩阵,而估计因子载荷矩阵的方法比较多,最常用的
是主成分法、主因子法和最大似然函数法。
#打开数据文件
> setwd(choose.dir())
> library(RODBC)
> z<-odbcConnectExcel(basename(choose.files()))
> sq<-sqlFetch(z,"Sheet1")
> d<-data.frame(sq$X1,sq$X2,sq$X3,sq$X4,sq$X5,sq$X6)
> fa<-factanal(d,factors = 2)
> fa
=================================================
十一.判别分析与聚类分析
1.判别分析
R语言中的MASS包中的lda()函数可以完成Fisher判别分析,格式如下
lda(formula,data,...,subset,na,action)
其中formula用法为总体来源~指标1+指标2+...,subset表示训练样本。
举例:从ST和非ST各抽取5个公司,再从证券市场抽取8个待判公司,请对这8家公司进行判别是ST还
是非ST。
#先打开训练样本数据文件
> setwd(choose.dir())
> library(RODBC)
> z<-odbcConnectExcel(basename(choose.files()))
> sq<-sqlFetch(z,"Sheet1")
#重新定义变量名称,并进行线性判别分析
> gp<-sq$group;y1<-sq$x1;y2<-sq$x2;y3<-sq$x3;y4<-sq$x4
> z<-lda(gp~y1+y2+y3+y4,data = sq,prior = c(1,1)/2)
#打开待判数据文件,并重新定义名称
> z1<-odbcConnectExcel(basename(choose.files()))
> newdata<-sqlFetch(z1,"Sheet1")
> y1<-newdata$x1;y2<-newdata$x2;y3<-newdata$x3;y4<-newdata$x4
> d<-data.frame(y1,y2,y,y4)
#带入上述判别结果进行判定
> predict(z,newdata = d)
$class
[1] A A A B B A A A
Levels: A B
$posterior
A B
1 0.78295713 2.170429e-01
2 1.00000000 1.060419e-14
3 1.00000000 1.327964e-14
4 0.09186256 9.081374e-01
5 0.26976912 7.302309e-01
6 0.99999998 1.541160e-08
7 1.00000000 6.465862e-10
8 0.99999781 2.185957e-06
$x
LD1
1 -0.2737539
2 -6.8658138
3 -6.8178086
4 0.4888592
5 0.2124756
6 -3.8381835
7 -4.5148253
8 -2.7809866
从$class可以看出,4,5公司为非ST,其余为ST,$x给出了判别函数的数值
2.聚类分析
利用R软件的hclust()函数可以完成系统聚类法,基本格式如下
hclust(d,method,mumbers)
其中d是有dist构成的距离结构,method是系统聚类方法,默认为最长距离法
举例:设有5个产品,每个产品测得一项指标x,值为:1,2,4,5,6,8,用最短距离法、最长距离法、
中间距离法、离差平方和法分别对5个产品进行分类
> x<-c(1,2,4.5,6,8)
> d<-dist(x)
> hc1<-hclust(d,method = "single")
> hc2<-hclust(d,method = "complete")
> hc3<-hclust(d,method = "median")
> hc4<-hclust(d,method = "ward.D")
> opar<-par(mfrow=c(2,2))
> plot(hc1,hang = 1)
> plot(hc2,hang = 1)
> plot(hc3,hang = 1)
> plot(hc4,hang = 1)
=================================================
十二、典型相关分析与对应分析
1.典型相关分析
典型相关关系是研究两组变量相关性的分析方法,基本思想是:首先在每组变量中找出变量的线性
组合,使其具有最大相关性,再在每组变量中找出第二对线性组合,使其分别与第一对线性组合不
相关,而第二对本身具有最大相关性,如此反复直到两组变量之间的相关性被提取完毕为止。而问
题也就转化为研究这些线性组合的最大相关性,从而减少研究变量的个数。
R软件中cancor函数可以完成典型相关分析,期格式如下:
cancor(x,y,xcenter=TRUE,ycenter=TRUE)
其中x,y为两组变量的矩阵,xcenter和ycenter为逻辑变量,TRUE表示将数据中心化。
举例:想分析25家企业业务部门和技术部门经理工作时间和员工工作时间的相关关系,使用典型相
关分析进行,数据已经做标准化处理
#选择excel数据
setwd(choose.dir())
library(RODBC)
z<-odbcConnectExcel(basename(choose.files()))
sq<-sqlFetch(z,"Sheet1")
#接下来使用典型相关分析
> ca<-cancor(sq[,2:3],sq[,4:5])
> ca
2.对应分析
可以使用MASS包中的corresp()函数完成对应分析,格式如下
corresp(x,nf=1)
其中x表示数据矩阵,nf=1表示计算因子个数。
举例:想研究某问卷中文化程度和就业观点两个变量的对应关系,先将其做分类汇总交叉表
#选择excel数据
setwd(choose.dir())
library(RODBC)
z<-odbcConnectExcel(basename(choose.files()))
sq<-sqlFetch(z,"Sheet1")
#定义行列名称
> df<-data.frame(sq$fcty,sq$ty,sq$bty,sq$fcbty)
> rownames(df)<-c("小学以下","小学","初中","高中","大学")
#进行对应分析并作图
> cor<-corresp(df,nf=2)
> biplot(cor)