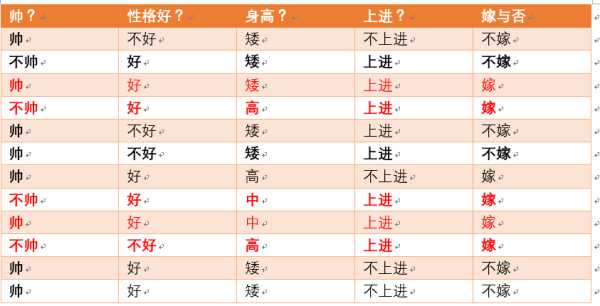
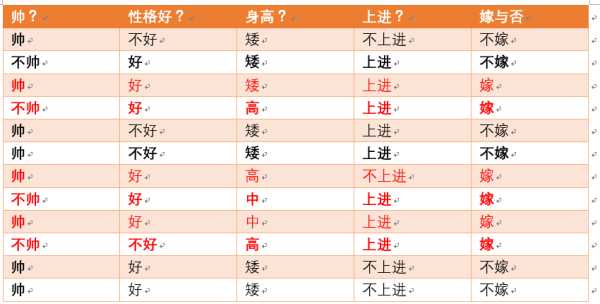
很傻很天真却很很好很强大的贝叶斯定理。。。
机器学习算法中,有种依据概率原则进行分类的朴素贝叶斯算 法,正如气象学家预测天气一样,朴素贝叶斯算法就是应用先 前事件的有关数据来估计未来事件发生的概率
基于朴素贝叶斯的垃圾邮件分类
BoW(词袋)模型
Bag-of-words model (BoW model) 最早出现在自然语言处理(Natural Language Processing)和信息检索(Information Retrieval)领域.。该模型忽略掉文本的语法和语序等要素,将其仅仅看作是若干个词汇的集合,文档中每个单词的出现都是独立的。BoW使用一组无序的单词(words)来表达一段文字或一个文档。
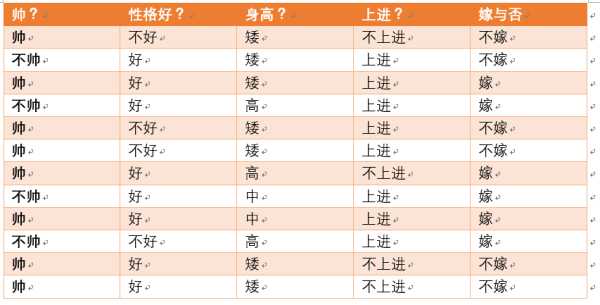
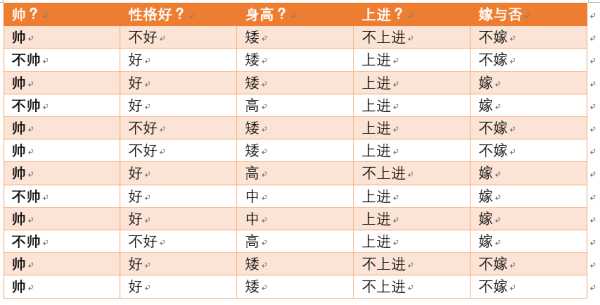
假设我们词库中只有四个单词I,don’t,love,you,分别用符号w1,w2,w3,w4意义对应表示,那么一封邮件就可以由这四个单词是否出现来表示,如:$w1\bigcap \neg w2 \bigcap w2 \bigcap w3$就表示文档I love you,而$w1\bigcap w2 \bigcap w2 \bigcap w3$就表示文档I don‘t love you。
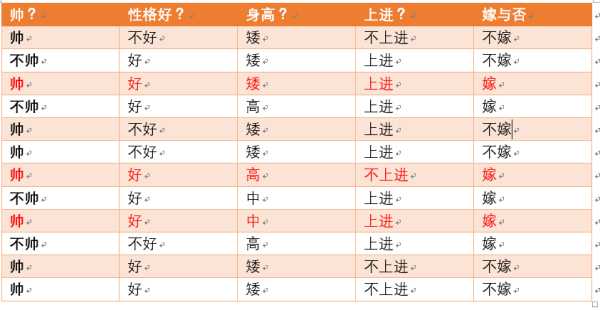
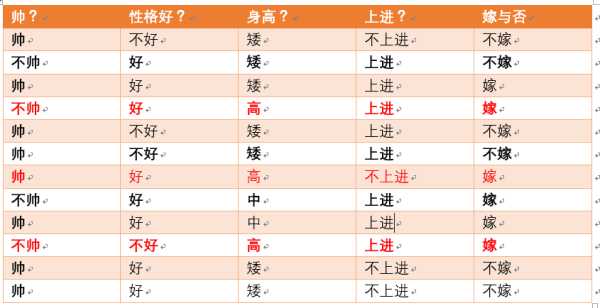
我们将单词出现的频率视为它出现的概率,如下图则P(Viagra)=5%。
如果我们知道P(垃圾邮件)和P(Viagra)是相互独立的, 则容易计算P(垃圾邮件&Viagra),即这两个事件同时发生 的概率。20%*5%=1%
独立事件我们可以简单的应用这个方法计算,但是在现实中, P(垃圾邮件)和P(Viagra)更可能是高度相关的,因此上述计算是不正确的,我们需要一个精确的公式来描述这两个事件之间的关系。
贝叶斯公式
垃圾邮件中的朴素贝叶斯公式
P(spam)为先验概率,P(spam|Viagra)为在Viagra单词出现后的后验概率。如果你不懂什么是先验概率和后验概率,请戳那些年被教科书绕晕的概率论基础
计算贝叶斯定理中每一个组成部分的概率,我们必须构造一个频率表
计算贝叶斯公式
P(垃圾邮件|Viagra)=P(Viagra|垃圾邮件)*P(垃圾邮件)/P(Viagra)=(4/20)*(20/100)/(5/100)=0.8
因此,如果电子邮件含有单词Viagra,那么该电子邮件是垃圾 邮件的概率为80%。所以,任何含有单词Viagra的消息都需 要被过滤掉。
当有额外更多的特征是,这一概念如何被使用呢?
利用贝叶斯公式,我们得到概率如下:
虽然我们写作时,相邻单词之间其实是有关联的,但是为了方便建立模型,我们假设单词的出现是相互独立,这也是Naive Bayes的Naive之处,很傻很天真,但是在实际应用中却发现其效果很好很强大。由于相互独立,那么就可以转化为接下来的公式:
? 分母可以先忽略它,垃圾邮件的总似然为:(4/20)*(10/20)*(20/20)*(12/20)*(20/100)=0.012
? 非垃圾邮件的总似然为:(1/80)*(66/80)*(71/80)*(23/80)*(80/100)=0.002
? 将这些值转换成概率,我们只需要一步得到垃圾邮件概率为 0.012/(0.012+0.002)=85.7%
存在的问题
另一个例子包含了4个单词的邮件呢?
? 我们可以计算垃圾邮件的似然如下:(4/20)*(10/20)*(0/20)*(12/20)*(20/100)=0
? 非垃圾邮件的似然为:(1/80)*(14/80)*(8/80)*(23/80)*(80/100)=0.00005
? 因此该消息是垃圾邮件的概率为0/(0+0.00005)=0
? 该消息是非垃圾邮件的概率为0.00005/(0+0.00005)=1
? 问题出在Groceries这个单词,所有单词Grogeries有效抵消或否决了所有其他的证据。
拉普拉斯估计
而这个错误的造成是由于训练量不足,会令分类器质量大大降低。为了解决这个问题,我们引入Laplace校准(这就引出了我们的拉普拉斯平滑),它的思想非常简单,就是对没类别下所有划分的计数加1,这样如果训练样本集数量充分大时,并不会对结果产生影响,并且解决了上述频率为0的尴尬局面。
引入拉普拉斯平滑的公式如下:
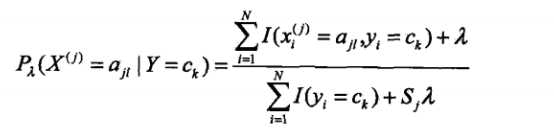
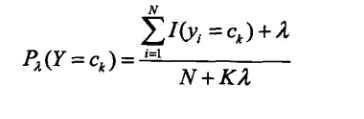
其中ajl,代表第j个特征的第l个选择,代表第j个特征的个数,K代表种类的个数。
为1,这也很好理解,加入拉普拉斯平滑之后,避免了出现概率为0的情况,又保证了每个值都在0到1的范围内,又保证了最终和为1的概率性质!
本文的情况是,由于词袋里一共是4个词,因此Sj = 4. 由于最终结果有两个分类,因此K = 2.
理解:
拉普拉斯估计本质上是给频率表中的每个计数加上一个较小的数,这样就保证了每一类中每个特征发生概率非零。
通常情况下,拉普拉斯估计中加上的数值设定为1,这样就保证每一类特征的组合至少在数据中出现一次。
? 然后,我们得到垃圾邮件的似然为:(5/24)*(11/24)*(1/24)*(13/24)*(20/100)=0.0004
? 非垃圾邮件的似然为:(2/84)*(15/84)*(9/84)*(24/84)*(80/100)=0.0001
? 这表明该消息是垃圾邮件的概率为80%,是非垃圾邮件的概率为20%。