caret包(Classification and Regression Training)是一系列函数的集合,它试图对创建预测模型的过程进行流程化。本系列将就数据预处理、特征选择、抽样、模型调参等进行介绍学习。
本文将就caret包中的数据预处理部分进行介绍学习。主要包括以下函数:model.matrix(),dummyVars(),nearZeroVar(),findCorrelation(),findLinearCombos(),preProcess(),classDist()
创建虚拟变量
创建虚拟变量的两个主要函数:model.matrix , dummyVars
model.matrix()
model.matrix(object, data = environment(object), contrasts.arg = NULL, xlev = NULL, ...)
其实,主要参数为object,一个公式;data就是引用的数据咯
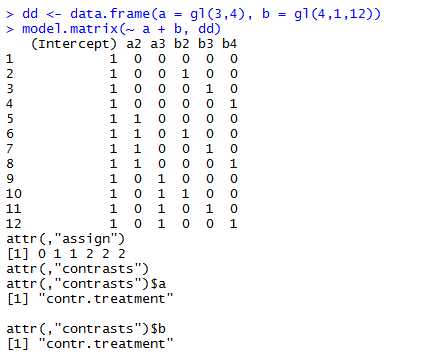
这里,式子中 ~后可以理解为要展开的数据(其实也可以有只有一个因子水平的数据,从而便于在展开数据的同时,cbind其他列的数据,从而得到接下来分析用到的数据),结果返回的是matrix类型
如上所示,有3个因子水平的a被展开成2列,其他一列被省掉,减少了多重共线性的困扰。但是,没搞明白,intercept是怎么得出来的?????
dummyVars()
dummyVars(formula, data, sep = ".", levelsOnly = FALSE, fullRank = FALSE, ...)
其用法跟model.matrix差不多,主要参数依旧是formula和data
不同的是
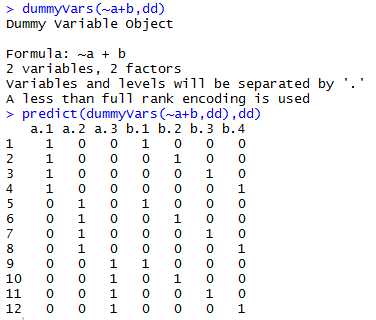
可以看出两点不同了:1. 需要调用predict函数才能显示矩阵 2. 是对所有level进行展开
此外,dummyVars还可以生成交互的展开

当然,还可以通过 sep = ";" 将a;1的形式, levelsOnly = TRUE 将a.1改成1, 但a.1:b.1改成1:1 不行 报错 情理之中,因为这样1:1的话就没有辨识度了,只有level是唯一不重复的,才可以如愿。
注意:因为dummyVars展开的没有截距(intercept),并且每个因子水平都有对应的虚拟变量,所以这些参数对于某些模型可能是不可用的,例如lm等
零方差和近似零方差特征变量
识别清除近似零方差的特征变量的原因:
- 在某些情况下,数据产生机制只创建具有单一值的特征变量(例如零方差特征变量)。这对于大多数模型(不包括树模型)来说,这可能造成模型的破坏,或者数据拟合的不稳定。
- 同样的,特征变量中可能有一些出现频率非常低的唯一值,当这样的数据使用交叉验证(cross-validation)或自助法(bootstrap)抽样或一些样本可能对模型有过度影响的时候,这些特征变量可能变成零方差的特征变量
识别此种特征变量的方法:
- 最大频率数值的频数比上第二频率数值的频数(称作频数比率(frequency ratio)),对于平衡的特征变量其值接近1,对于高度不平衡的数据其值会非常大
- 唯一值比例就是唯一值的个数除以样本的总数再乘以100, 它随着数据粒度的增大而几近于0。
如果频数比率大于预先设定的阈值,并且唯一值的比例小于一个阈值,我们可以认为这个特征变量为近似零方差。
caret包中提供了函数:nearZeroVar()
nearZeroVar(x, freqCut = 95/5, uniqueCut = 10, saveMetrics = FALSE, names = FALSE, foreach = FALSE, allowParallel = TRUE)
参数解释:
- x 是一个数值型向量、矩阵或data frame,freqCut是频数比率阈值,uniqueCut是唯一值比例阈值
- saveMetrics是一个逻辑值,false时返回的是近零特征的位置,true时,返回特征信息的data frame
- name 逻辑值,false时,返回列的索引,true时返回列的名字
- foreach 是否调用foreach包,若为ture,将使用更少的内存
- allowPatallel 是否通过foreach包进行并行计算,若为true,将占用更多内存,但执行时间更短
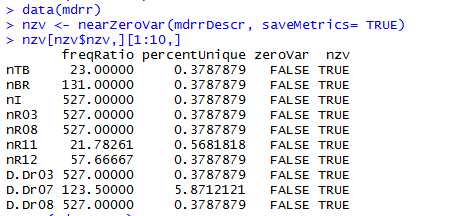
返回的参数解释:
freqRatio 频数比率 percentUnique 唯一值比率 zeroVar 是否仅有一个值 nzv 是否是近零方差特征
清除近零方差特征变量:

识别相关的特征变量
有些模型依赖与相关的特征变量(像偏最小二乘法(pls,partial least-squares regression)),而有些模型能够得益于变量之间的相关性减少。
findCorrelation(x, cutoff = 0.9, verbose = FALSE, names = FALSE, exact = ncol(x) < 100)
参数解释:
- x 是一个相关性矩阵
- cutoff 是相关性绝对值的阈值
- verbose 是否显示details
- names 是否返回列名。false时,返回列的索引
- exact 逻辑值,平均相关性是否在每一步重新计算。当维数比较大时,exact calculations将清除更少的特征,且比较慢
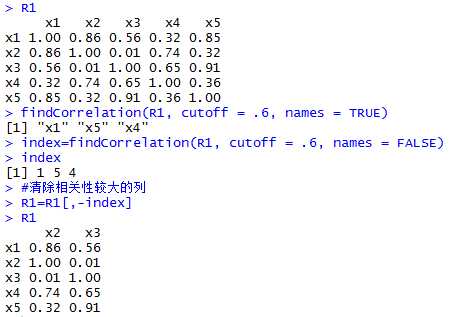
线性相关性
函数findLinearCombos使用QR分解来枚举线性组合的集合(如果存在的话)
findLinearCombos(x) 只有一个参数x,x是一个数值矩阵
返回一个列表,含有两项:
- linearCombos 若有线性相关的,显示列索引向量
- remove 为去除线性相关性,应去除的列索引

preProcess函数
preProcess函数可以对特征变量施行很多操作,包括中心化和标准化。preProcess函数每次操作都估计所需要的参数,并且由predict.preProcess 应用于指定的数据集。
preProcess(x, method = c("center", "scale"), thresh = 0.95,
pcaComp = NULL, na.remove = TRUE, k = 5,
knnSummary = mean, outcome = NULL, fudge = 0.2,
numUnique = 3, verbose = FALSE, freqCut = 95/5,
uniqueCut = 10, cutoff = 0.9, ...)
x 是一个矩阵或数据框。非数值型的变量是被允许的,但是将被忽略
method 处理类型的字符串向量。常见的几种如下:
- center 中心化,即减去自变量的平均值
- scale 标准化,即除以自变量的标准差,变换后值域为[0,1]。如果新样本值大于或小于训练集中值,则值将超出此范围。
- BoxCox 变换,用于自变量,简单,与幂变换一样有效
- YeoJohnson 与BoxCox 变换相似,但是它的自变量可以是0或负数,而BoxCox只能是正数
- expoTrans 指数变换(exponential transformations)也可以被用于正数或负数
- zv 识别并清除掉只含有一个值的数值型自变量
- nzv 相当于应用nearZeroVar,清除近零方差的自变量
- corr 寻找并过滤掉具有高相关性的自变量,参见findCorrelation
这些方法的运行顺序是:zero-variance filter, near-zero variance filter, correlation filter, Box-Cox/Yeo-Johnson/exponential transformation, centering, scaling, range, imputation, PCA, ICA then spatial sign.
thresh PCA的累积方差比

其实,preProcess的功能很强大,据说还可以对数据进行插补缺失值(K近邻,袋装树bagged tree)
笔者还未深入研究,在此不一一叙述
类别距离计算
classDist 函数计算训练集的类别质心和协方差矩阵,从而确定样本与每个类别质心的马氏距离。
classDist(x, y, groups = 5, pca = FALSE, keep = NULL, ...)
predict(object, newdata, trans = log, ...) 默认的距离取对数,但是这可以通过predict.classDist的参数trans来改变
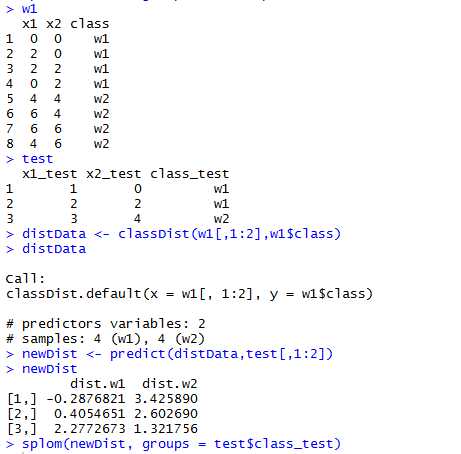
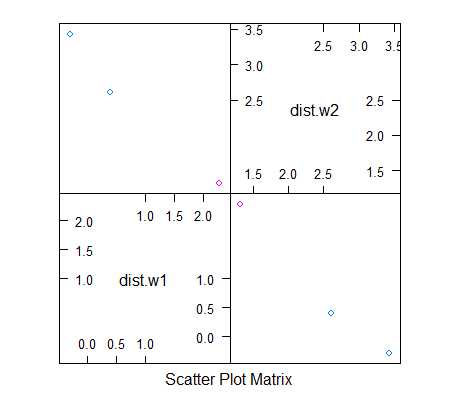
可见,上图关于对角线对称,且将test分为两类,蓝色一类,红色一类。
参考: