Golang 数据结构实现之 二叉树
二叉树的理论知识,应该都比较了解了,下文不再详细介绍二叉树的基本知识。
在二叉树中具有以下重要性质:
1.在二叉树的第i层上最多有(2的i次方)个结点。
2.高度为h的二叉树至多有(2的h+1次方-1)个结点。
3.对任何一棵二叉树,如果其终端结点(叶子结点)数为n0,度为2的结点数为n2,则n0 = n2 + 1。
下面就直接贴出golang的二叉树代码,由binaryTreeNode.go和binaryTree.go两个文件组合:
binaryTreeNode.go:
(
package tree
import (
"math"
)
//二叉树节点
type BinTreeNode struct {
data interface{} //数据域
parent *BinTreeNode //父节点
lChild *BinTreeNode //左孩子
rChild *BinTreeNode //右孩子
height int //以该结点为根的子树的高度
size int //该结点子孙数(包括结点本身)
}
func NewBinTreeNode(e interface{}) *BinTreeNode {
return &BinTreeNode{data: e, size: 1}
}
//获得节点数据
func (this *BinTreeNode) GetData() interface{} {
if this == nil {
return nil
}
return this.data
}
//设置节点数据
func (this *BinTreeNode) SetData(e interface{}) {
this.data = e
}
//判断是否有父亲
func (this *BinTreeNode) HasParent() bool {
return this.parent != nil
}
//获得父亲节点
func (this *BinTreeNode) GetParent() *BinTreeNode {
if !this.HasParent() {
return nil
}
return this.parent
}
//设置父亲节点
func (this *BinTreeNode) setParent(p *BinTreeNode) {
this.parent = p
// this.parent.SetHeight() //更新父结点及其祖先高度
// this.parent.SetSize() //更新父结点及其祖先规模
}
//断开与父亲的关系
func (this *BinTreeNode) CutOffParent() {
if !this.HasParent() {
return
}
if this.IsLChild() {
this.parent.lChild = nil //断开该节点与父节点的连接
} else {
this.parent.rChild = nil //断开该节点与父节点的连接
}
this.parent = nil //断开该节点与父节点的连接
this.parent.SetHeight() //更新父结点及其祖先高度
this.parent.SetSize() //更新父结点及其祖先规模
}
//判断是否有左孩子
func (this *BinTreeNode) HasLChild() bool {
return this.lChild != nil
}
//获得左孩子节点
func (this *BinTreeNode) GetLChild() *BinTreeNode {
if !this.HasLChild() {
return nil
}
return this.lChild
}
//设置当前结点的左孩子,返回原左孩子
func (this *BinTreeNode) SetLChild(lc *BinTreeNode) *BinTreeNode {
oldLC := this.lChild
if this.HasLChild() {
this.lChild.CutOffParent() //断开当前左孩子与结点的关系
}
if lc != nil {
lc.CutOffParent() //断开lc与其父结点的关系
this.lChild = lc //确定父子关系
lc.setParent(this)
this.SetHeight() //更新当前结点及其祖先高度
this.SetSize() //更新当前结点及其祖先规模
}
return oldLC
}
//判断是否有右孩子
func (this *BinTreeNode) HasRChild() bool {
return this.rChild != nil
}
//获得右孩子节点
func (this *BinTreeNode) GetRChild() *BinTreeNode {
if !this.HasRChild() {
return nil
}
return this.rChild
}
//设置当前结点的右孩子,返回原右孩子
func (this *BinTreeNode) SetRChild(rc *BinTreeNode) *BinTreeNode {
oldRC := this.rChild
if this.HasRChild() {
this.rChild.CutOffParent() //断开当前左孩子与结点的关系
}
if rc != nil {
rc.CutOffParent() //断开rc与其父结点的关系
this.rChild = rc //确定父子关系
rc.setParent(this)
this.SetHeight() //更新当前结点及其祖先高度
this.SetSize() //更新当前结点及其祖先规模
}
return oldRC
}
//判断是否为叶子结点
func (this *BinTreeNode) IsLeaf() bool {
return !this.HasLChild() && !this.HasRChild()
}
//判断是否为某结点的左孩子
func (this *BinTreeNode) IsLChild() bool {
return this.HasParent() && this == this.parent.lChild
}
//判断是否为某结点的右孩子
func (this *BinTreeNode) IsRChild() bool {
return this.HasParent() && this == this.parent.rChild
}
//取结点的高度,即以该结点为根的树的高度
func (this *BinTreeNode) GetHeight() int {
return this.height
}
//更新当前结点及其祖先的高度
func (this *BinTreeNode) SetHeight() {
newH := 0 //新高度初始化为0,高度等于左右子树高度加1中的大者
if this.HasLChild() {
newH = int(math.Max(float64(newH), float64(1+this.GetLChild().GetHeight())))
}
if this.HasRChild() {
newH = int(math.Max(float64(newH), float64(1+this.GetRChild().GetHeight())))
}
if newH == this.height {
//高度没有发生变化则直接返回
return
}
this.height = newH //否则更新高度
if this.HasParent() {
this.GetParent().SetHeight() //递归更新祖先的高度
}
}
//取以该结点为根的树的结点数
func (this *BinTreeNode) GetSize() int {
return this.size
}
//更新当前结点及其祖先的子孙数
func (this *BinTreeNode) SetSize() {
this.size = 1 //初始化为1,结点本身
if this.HasLChild() {
this.size += this.GetLChild().GetSize() //加上左子树规模
}
if this.HasRChild() {
this.size += this.GetRChild().GetSize() //加上右子树规模
}
if this.HasParent() {
this.parent.SetSize() //递归更新祖先的规模
}
}
binaryTree.go:
package tree
import (
"container/list"
)
//二叉树
type binaryTree struct {
root *BinTreeNode //根节点
height int
size int
}
func NewBinaryTree(root *BinTreeNode) *binaryTree {
return &binaryTree{root: root}
}
//获得二叉树总结点数
func (this *binaryTree) GetSize() int {
return this.root.size
}
//判断二叉树是否为空
func (this *binaryTree) IsEmpty() bool {
return this.root != nil
}
//获得二叉树根节点
func (this *binaryTree) GetRoot() *BinTreeNode {
return this.root
}
//获得二叉树高度,根节点层为0
func (this *binaryTree) GetHeight() int {
return this.root.height
}
//获得第一个与数据e相等的节点
func (this *binaryTree) Find(e interface{}) *BinTreeNode {
if this.root == nil {
return nil
}
p := this.root
return isEqual(e, p)
}
func isEqual(e interface{}, node *BinTreeNode) *BinTreeNode {
if e == node.GetData() {
return node
}
if node.HasLChild() {
lp := isEqual(e, node.GetLChild())
if lp != nil {
return lp
}
}
if node.HasRChild() {
rp := isEqual(e, node.GetRChild())
if rp != nil {
return rp
}
}
return nil
}
//先序遍历,并保存在链表里
func (this *binaryTree) PreOrder() *list.List {
traversal := list.New()
preOrder(this.root, traversal)
return traversal
}
func preOrder(rt *BinTreeNode, l *list.List) {
if rt == nil {
return
}
l.PushBack(rt)
preOrder(rt.GetLChild(), l)
preOrder(rt.GetRChild(), l)
}
//中序遍历,并保存在链表里
func (this *binaryTree) InOrder() *list.List {
traversal := list.New()
inOrder(this.root, traversal)
return traversal
}
func inOrder(rt *BinTreeNode, l *list.List) {
if rt == nil {
return
}
inOrder(rt.GetLChild(), l)
l.PushBack(rt)
inOrder(rt.GetRChild(), l)
}
//后序遍历,并保存在链表里
func (this *binaryTree) PostOrder() *list.List {
traversal := list.New()
postOrder(this.root, traversal)
return traversal
}
func postOrder(rt *BinTreeNode, l *list.List) {
if rt == nil {
return
}
postOrder(rt.GetLChild(), l)
postOrder(rt.GetRChild(), l)
l.PushBack(rt)
}上述遍历的过程显然是一个递归的过程,算法中是将结点加入链接表list的尾部作为对结点的访问,该操作只需要常数时间即可完成。在算法的递归执行过程中,每个结点访问且仅被访问一次,因此算法的时间复杂度T(n) = Ο(n)。对于中序和后序遍历的递归算法也是如此,即中序和后序递归算法的时间复杂度也是Ο(n)。
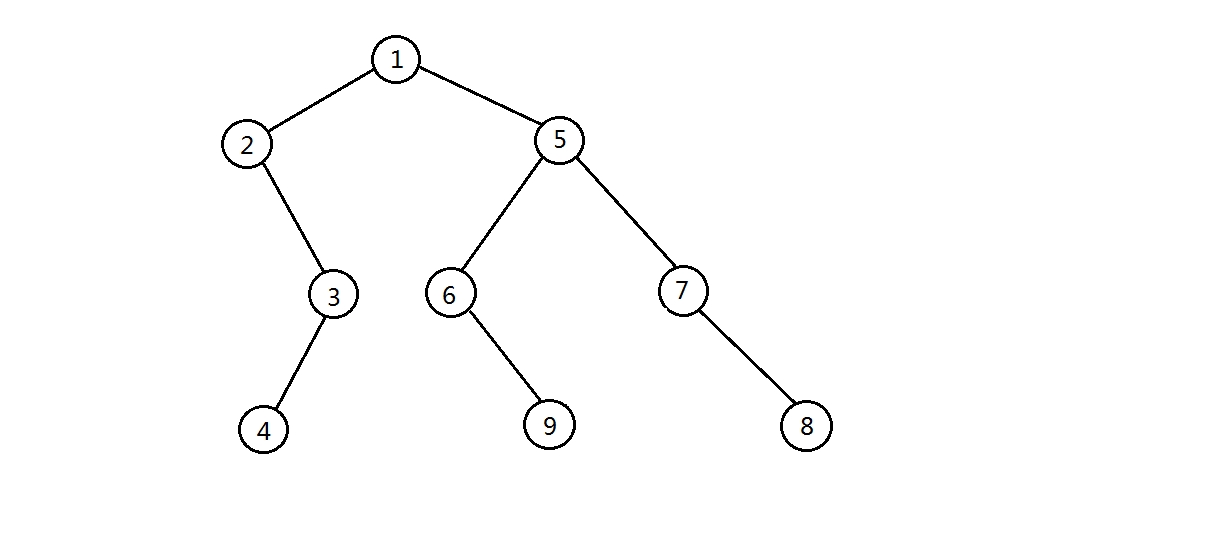
下面做下测试,创建这么一棵二叉树:
测试代码:
package main
import (
"dataStructures/tree"
"fmt"
)
func main() {
a := tree.NewBinTreeNode(1)
tree1 := tree.NewBinaryTree(a)
a.SetLChild(tree.NewBinTreeNode(2))
a.SetRChild(tree.NewBinTreeNode(5))
a.GetLChild().SetRChild(tree.NewBinTreeNode(3))
a.GetLChild().GetRChild().SetLChild(tree.NewBinTreeNode(4))
a.GetRChild().SetLChild(tree.NewBinTreeNode(6))
a.GetRChild().SetRChild(tree.NewBinTreeNode(7))
a.GetRChild().GetLChild().SetRChild(tree.NewBinTreeNode(9))
a.GetRChild().GetRChild().SetRChild(tree.NewBinTreeNode(8))
node2 := a.GetLChild()
node9 := a.GetRChild().GetLChild().GetRChild()
fmt.Println("结点2是叶子结点吗? ", node2.IsLeaf())
fmt.Println("结点9是叶子结点吗? ", node9.IsLeaf())
fmt.Println("这棵树的结点总数:", tree1.GetSize())
l := tree1.InOrder()//中序遍历
for e := l.Front(); e != nil; e = e.Next() {
obj, _ := e.Value.(*tree.BinTreeNode)
fmt.Printf("data:%v\n", *obj)
}
result := tree1.Find(6)
fmt.Printf("结点6的父节点数据:%v\t结点6的右孩子节点数据: %v\n", result.GetParent().GetData(), result.GetRChild().GetData())
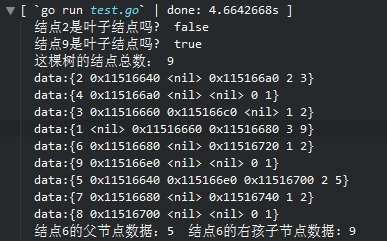
} 结果:
看下中序遍历后,list内存储节点的顺序:2,4,3,1,6,9,5,7,8.符合这棵树中序遍历的结果。
本文出自 “Programming in XMU” 博客,请务必保留此出处http://liuxp0827.blog.51cto.com/5013343/1378672
文章来自:http://liuxp0827.blog.51cto.com/5013343/1378672