塔吊配重计算说明

1 问题的数学抽象

1.1 问题总结

有m种类型的总配重，重量分别为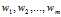，每种类型总配重由若干个砖块组成。

有n种型号的砖块，每种型号砖块的质量分别为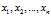(需要求解的)。

对于某种类型的总配重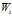，每种型号的砖块数量为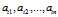(需要求解的)。

总配重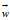，每种砖块质量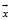，每个总配重对应的每种砖块的数量A，满足方程，即

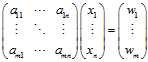（1）

1.2 相关限制条件

砖块的型号一般是2-3种，即x大概是2、3个，但方程组的数量一般超过3个，这里只针对方程组较多（m>n）时求解A和x。

1）每种类型的总配重需要的砖块数量不超过5、6块，即

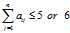（2）

2）对于每种型号砖块的重量，差异不能太大，可以用最重的砖块和最轻的砖块质量差值来量化。（该限制条件主要是为了防止求解出的砖块重量差异太大，例如求解方程结果可能一种砖块1吨，另一种15吨，任满足要求但差异太大）。

3）容许总配重略微重一些，具体值自己给定。

?

2 程序求解的思路

2.1 用实例化的公式展示

????假设一个系列的塔吊有6种型号的起重量，即m=6，砖块的类型设为3种，n=3。得到的方程组为：

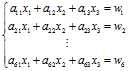（3）

求方程左边的所有量。这是欠约束方程组，而且是非线性的，这里采用列举的方法求解。

求解步骤大致为：

?

Step1 列举出系数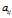满足（2）式所有组合，例如1 2 2，3 0 0等等。

Step2 在所有的系数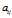的组合中取3组（每种取法都需要用一次），总配重系数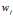中取3组（即只选了3个方程），由此可以计算出每种类型砖块的重量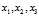的值。

Step3 剩下的没选中的3个方程中x成为已知的，需要计算系数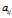，系数的所有可能已经在Step1中列举出，在列举出的集合中搜索满足要求的系数，如果三个方程都能满足，就得到一组合理的解，保存。继续Step2。