logistic回归算法的损失函数：binary_crossentropy（二元交叉熵）
假设函数：
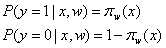
更为一般的表达式：![技术分享图片]()
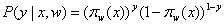（1）似然函数：
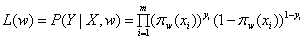
对数似然函数：
如果以上式作为目标函数，就需要最大化对数似然函数，我们这里选择最小化负的对数似然函数
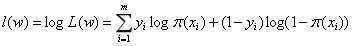
对J(w)求极小值，对![技术分享图片]()
求导
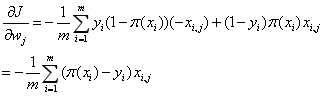
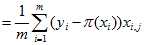（4）上述中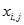 
表示第i个样本的第j个属性的取值。
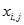表示第i个样本的第j个属性的取值。于是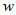
的更新方式为：
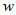的更新方式为：
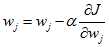（5）将（5）式带入（4）式，得：
梯度下降GD![技术分享图片]()
的更新方式,使用全部样本：
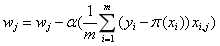（6）当样本不多的时候，可以选择这个方法
随机梯度下降：
每次只取一个样本，则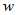
![技术分享图片]()
的更新方式：
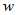
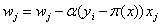（7）
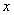
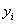是其真实值，
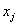是这个样本的第j个属性随机平均梯度下降法（sag，Stochasitc Average Gradient ）：
该算法是选取一小部分样本梯度的平均值来更新权重（其中n<m,m为样本数）
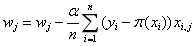（8）SGD和GD算法的折中
小结：
在尝试写一些机器学习相关的笔记，先写下一篇，欢迎讨论~
文章来自：https://www.cnblogs.com/sunrise-keephungary/p/10056027.html