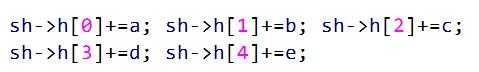SHA-1加密算法原理

SHA-1是一种能够根据上限为2^64位的消息计算出160比特的散列值的单向散列函数，它的分组及对数据的填充方式与MD5是一样的，512位为1组，填充数据时先填1，后面填0，一直填满448位，最后64位表示原始数据长度。

1. SHA-1： 填充

以Hello.这条长度为6字节的消息进行填充。

Hello. = 48 65 6C 6C 6F 2E，写成二进制形式如下：

01001000 01100101 01101100 01101100 01101111 00101110

原始数据长度为6字节(48位)

①. 对数据的填充，一直填满448位

01001000 01100101 01101100 01101100 01101111 00101110 1  (先填充1个1)

01001000 01100101 01101100 01101100 01101111 00101110 10000000000000000000000........ (再填充0，一直填满448位)

②.  在最末位添加原始数据长度(6字节)

01001000 01100101 01101100 01101100 01101111 00101110 10000000000000000000000........ 00000000 (假设到这里填满448位了)

000000000000000000000000000000000000000000000000000000000110000 (末尾增加原始数据长度48位，二进制形式添加)

到此，总共的数据就为512位了

2. SHA-1： 计算W0~W79

完成数据的填充后，我们将以输入分组为单位进行下面的处理，这一步要对每个输入分组计算80个32位的值(W0~W79)，首先将输入分组的512位分为32位*16组，并将它们命名为W0~W15，然后，剩下的W16~W79的计算方法如下：

W16 = (W0 ^ W2 ^ W8 ^ W13) 循环左移1位

即：

Wt = (Wt - 16 ^ Wt - 14 ^ Wt - 8 ^ Wt - 3) 循环左移1位

完成后，W0~W79的数据就生成完成了。

3. SHA-1： 分组处理

接下来，对输入分组进行80个步骤的处理，目的是根据输入分组的信息来改变内部状态。

在对分组处理时，SHA-1中常数Kt及Ht：

SHA-1使用了f0, f1, .... f79这样的一个逻辑函数序列，每一个ft对3个32位双字B,C,D进行操作，产生一个32位双字的输出。

对W0~W19的处理：

对W20~W39的处理：

对W40~W59的处理：

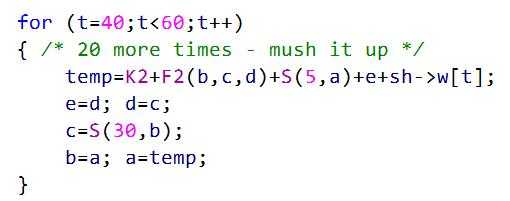
对W60~W79的处理：

在一个步骤完成之后，缓冲区a,b,c,d的内容会被分别复制到b,c,d,e中(其中b要循环左移30位之后再复制)，而缓冲区e的内容则会与其他缓冲区的内容以及Wt、Kt相加之后再复制到缓冲区a中。

最终将循环80个步骤的值与原始相加，即更新原始的5个H常量，得到最终160位的消息摘要。