下列是5个城市的交通图,城市之间的连线旁边的数字是城市之间路程的费用。要求从A城出发,经过其它各城市一次且仅一次,最后回到A城,请找出一条最优线路。
这个问题又称为旅行商问题(travelling salesman problem, TSP)或货郎担问题,是一个较有普遍性的实际应用问题。根据数学理论,对n个城市的旅 行商问题,其封闭路径的排列总数为(n!)/n=(n-1)! 其计算量相当大。例如,当n=20时,要穷举其所有路径,即使用一个每秒一亿次的计算机来算也需要350年的时间。因此,对这类问题只能用搜索的方法来解决。下图是对图4-32按代价一致搜(最小代价搜索)所得到的搜索树树中的节点为城市名称,节点边上的数字为该节点的代价g其计算公式为
g(ni+1)=g(ni)+c(ni, ni+1)
节点的边代价。
其中,c(ni,ni+1)为节点ni到ni+1节点的边代价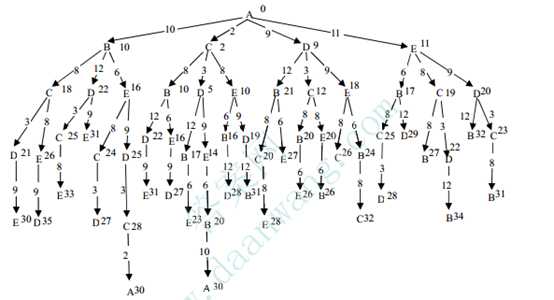
可以看出,其最短路经是:A-C-D-E-B-A 或A-B-E-D-C-A 其实,它们是同一条路经
文章来自:http://www.cnblogs.com/chenxiangzhou/p/4358367.html