【整合】数据平滑
问题描述
N-gram存在问题，训练语料毕竟是有限的，这样导致很多事件，如trigram中，w1 w2 w3根本没有出现过。根据最大似然估计，这些事件的概率为零。然而这些事件的真实概率并不一定为零。这个问题被成为数据稀疏问题。
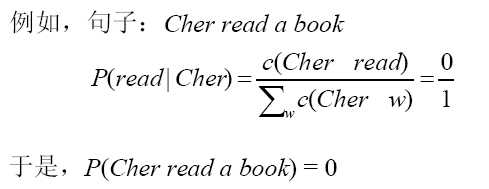
-- MLE给训练样本中未观察到的事件赋以0概率。
-- 若某n-gram在训练语料中没有出现,则该n-gram的概率必定是0。
-- 解决的办法是扩大训练语料的规模。但是无论怎样扩大训练语料，都不可能保证所有的词在训练语料中均出现。
-- 由于训练样本不足而导致所估计的分布不可靠的问题，称为数据稀疏问题。
-- 在NLP领域中，数据稀疏问题永远存在，不太可能有一个足够大的训练语料，因为语言中的大部分词都属于低频词。
Zipf 定律：
（1）告诉我们语言中只有很少的常用词，语言中大部分词都是低频词(不常用的词)。
（2）解释是Principle of Least effort(讲话的人和听话的人都想省力的平衡)；说话人只想使用少量的常用词进行交流；听话人只想使用没有歧义的词(量大低频)进行交流。
（3）对于语言中的大多数词，它们在语料中的出现是稀疏的.只有少量词语料库可以提供它们规律的可靠样本。
定义
把在训练样本中出现多的事件的概率适当减小，把减小得到的概率密度分配给训练语料中没有出现过的事件。这个过程有时也称为减值（Discounting）。
--减值法
修改训练样本中的事件的实际计数，是样本中不同时间的概率之和小于1，剩余的概率量分配给未见概率。
--调整方法：最大似然规则
（1）他可保证模型中任何概率均不为0；
（2）数据平滑使模型参数概率分布趋向于更加均匀。低概率（包括0概率）被调高，高概率被调低。
--数据平滑技术
（1）加法平滑
Add-one
1.每一种情况出现的次数加1。
2.规定任何一个n-gram在训练语料至少出现一次（即规定没有出现过的n-gram在训练语料中出现了一次），则: new_count(n-gram) = old_count(n-gram) + 1
3.没有出现过的n-gram的概率不再是0
例如，对于uni-gram，设w1, w2, w3 三个词，概率分别为：1/3, 0, 2/3，加1后情况？
2/6, 1/6, 3/6
Add-delta平滑
Lidstone’s 不是加1,而是加一个小于1的正数 ， 通常= 0.5，此时又称为Jeffreys-Perks Law或ELE 效果比Add-one好，但是仍然不理想。
（2）Good-turning平滑
【来自wiki】
Good-Turing基本思想是:用观察计数较高的N元语法数重新估计概率量的大小，并把它指派给那些具有零计数或者较低计数的N元语法。
涉及的符号含义为:
：某个N元语法出现的频数。
:出现次数为c的 N-gram 词组的个数，是频数的频数即：
:Good-Turing平滑计数:
Katz所做改进
Katz认为,实际上，并非对于所有的计数C都使用打折估计的计数是可靠的，假定对较大的计数是可靠的(对于某个阈值k，c>k),他建议取k的值为5，即：
当引入某个K时，C*的正确等式为：（Katz，1987）
Good-Turing常常与Katz回退法一起使用，实际上所有的回退语言模型都必须打折。其他打常见平滑法还有:加1平滑，Witten-Bell打折法，留存估计，删除估计，Add-delta等。
【解释】基本思想：利用高频率n-gram的频率调整低频的n-gram的频率。
具体操作：假设N 是样本数据的大小， nr是在N元模型的训练集中正好出现r 次的事件的数目（在这里，事件为N元对 ）,nr表示有多少个N元对出现了r次
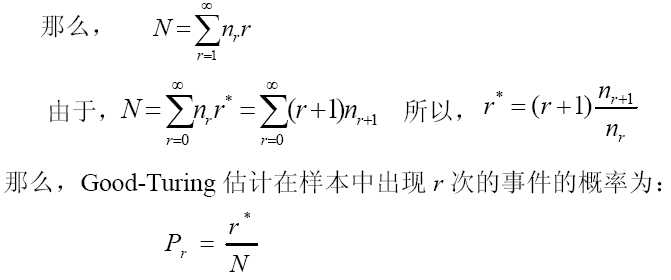
Good-Turing估计适合单词量大并具有大量的观察数据的情况下使用，在观察数据不足的情况下，本身出现次数就是不可靠的，利用它来估计出现次数就更不可靠了。缺乏利用低元模型对高元模型进行线性插值的思想。
【例子】
为了更好地理解古德-图灵（Good-Turing）估计法，以一个例子来讲解。
训练集合：T={<s>what is it what is small?}|T|=8
验证集合：V={what is it small ? <s> flying birds are a bird.}, |V|=12
在训练集合上，我们得到：p(<s>)=p(it)=p(small)=p(?)=0.125, p(what)=p(is)=0.25，其他为0
如果不经过平滑处理，则验证集上两句子的概率分别为：p(what is it?)=（0.25*2）*（0.125*2）≈0.001 p(it is flying.)=0.125*0.25*（0*2）=0
现在用古德-图灵算法进行平滑处理，如下：
首先计算，各发生r次N元组类别的数目，依次为N(0)=6,N(1)=4,N(2)=2,N(i)=0 ,i>2:
其次，重新估计各概率值。
对于发生0次的事件概率：Pr(.)=p(flying)=p(birds)=p(are)=p(bird)=p(a)=(0+1)*N(0+1)/(8*N(0))=1*4/(8*6)≈0.083
对于发生1次的时间概率：Pr(it)=p(<s>)=p(small)=p(?)=(1+1)*N(1+1)/(8*N(1))=2*2/(8*4)=0.125
对于发生两次的时间概率：Pr(what)=Pr(is)=(2+1)*N(2+1)/(8*N(2))=3*0/(8*2)=0: 保持原值0.25
归一化处理，6*P0+4*P1+2*P2=1.5。.
所以，归一化处理后，p’(it)=p’(<s>)=p’(small)=p’(?)= 0.125/1.5 ≈0.08, p’(what)=p’(is)= 0.25/1.5 ≈0.17,
p’(.)=p’(birds)=p’(are)=p’(bird)=p’(a) = 0.083/1.5 ≈0.06
因此：p’(what is it?)=（0175*2）*（0.08*2）≈0.0002 p’(it is flying.) ≈ 0.08*0.17*（0.06*2）≈0.00004
（3）Backing-off平滑
（4）Jelinek-mercer平滑
线性插值平滑（Linear Interpolation Smoothing）方法通常也被称作Jelinek-Mercer 平滑。Jelinek 和Mercer 在1980 年首先提出了这种数据平滑算法的思想，Brown 在1992 年给出了线性插值的平滑公式：
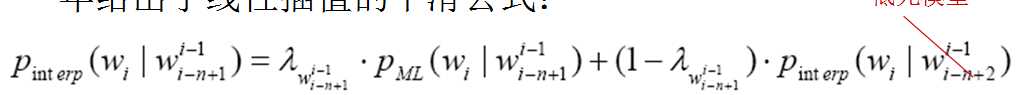
该参数平滑技术的基本思想是利用低元n-gram 模型对高元n-gram 模型进行线性插值。用降元的方法来弥补高元的数据稀疏问题，数据估计有一定的可靠性。但是参数估计较困难。
（5）Katz平滑
（6）Church-gale平滑