二路归并排序
二路归并排序主要运用了“分治算法”,分治算法就是将一个大的问题划分为n个规模较小而结构相似的子问题。
这些子问题解决的方法都是类似的,解决掉这些小的问题之后,归并子问题的结果,就得到了“大”问题的解。
二路归并排序主旨是“分解”与“归并”
分解:
1.将一个数组分成两个数组,分别对两个数组进行排序。
2.循环第一步,直到划分出来的“小数组”只包含一个元素,只有一个元素的数组默认为已经排好序。
归并:
1.将两个有序的数组合并到一个大的数组中。
2.从最小的只包含一个元素的数组开始两两合并。此时,合并好的数组也是有序的。
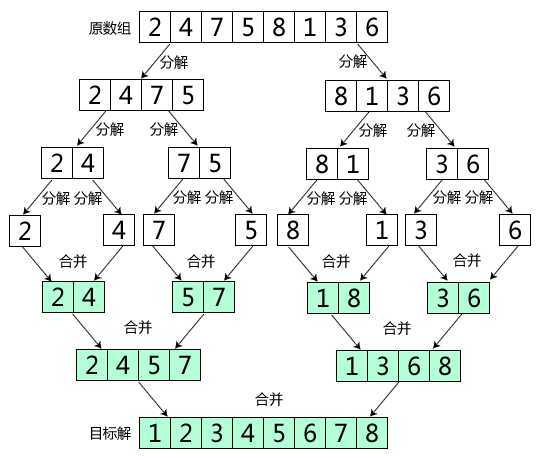
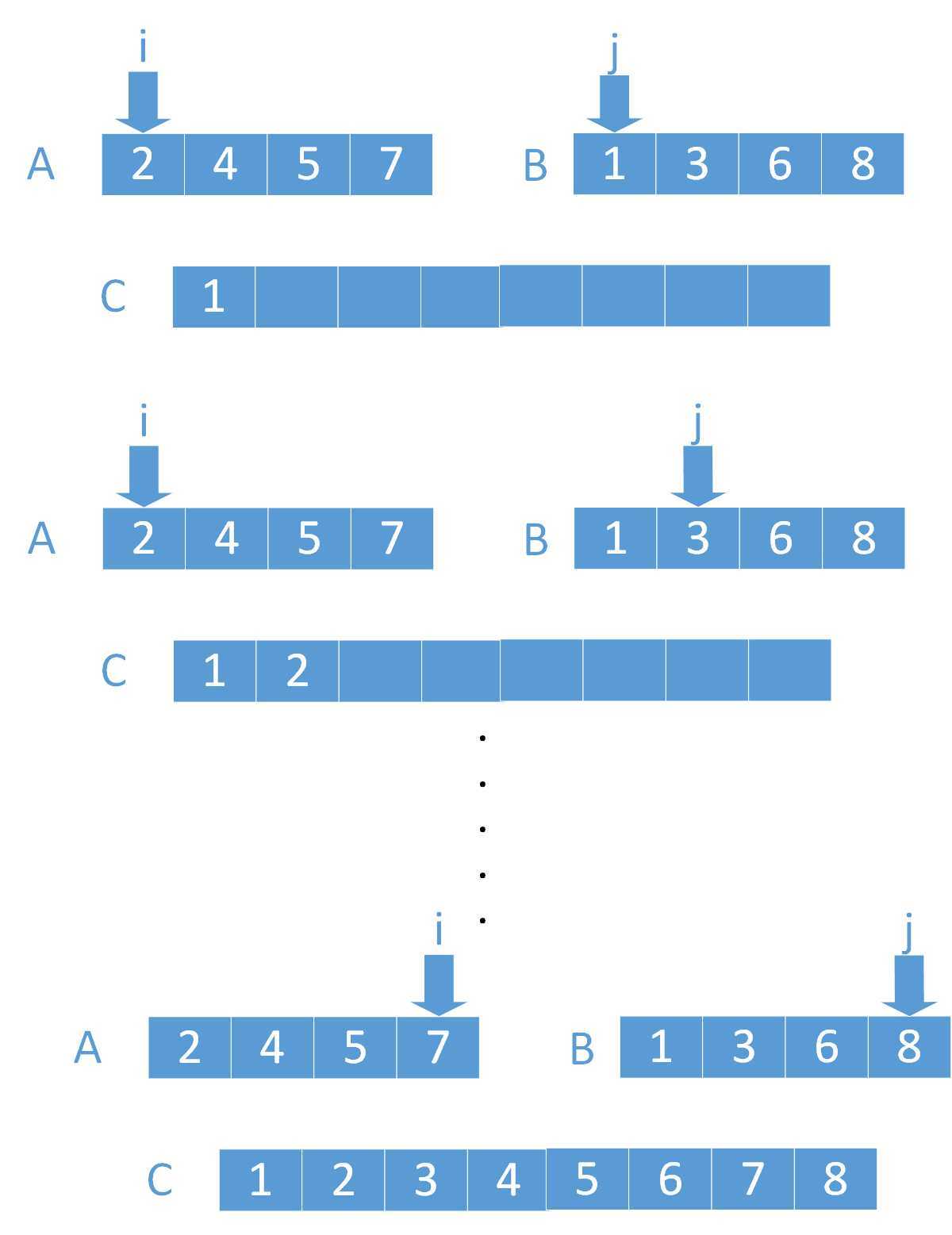
图1. 归并排序过程 图2. 合并两个有序数组
举例说明:
1.图中原始数组为{2,4,7,5,8,1,3,6},数组中元素的个数为8个。首先将8个元素的数组二分,每次分解后,
数组中元素的数目为原数组的一般。直到分解为只含有一个元素的数组。
2.将小的数组按序合并,每次合并后数组的大小为上层数组的一倍。此时数组中的元素都是按序排列的。
3.在合并两个有序数组。如图2
(1) 合并时,有两个指针分别指向有序数组A和B的起始元素,比较指针所指元素的大小,如果A[i]较小,则将A[i]
存入数组C中,并且将i后移。循环比较i和j所指的元素。
(2)当一个数组A的元素全部排之后,数组B中的指针就并没有指向B的末尾位置,将B中剩余元素全部存入到C中。
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 void Merge(int array[], int p, int q, int r); 5 void MergeSort(int array[], int p, int q); 6 7 int main() 8 { 9 int array[8] = {5,2,4,7,1,3,2,6}; 10 int i = 0; 11 12 MergeSort(array, 0, 7); 13 //Merge(array, 0, 2, 6); 14 15 for(i; i < 8; i++) 16 printf("%d ", array[i]); 17 return 0; 18 } 19 20 //合并过程中 p<=q<r 21 void Merge(int array[], int p, int q, int r) 22 { 23 int n1 = q - p + 1; 24 int n2 = r - q; 25 26 int *L; 27 L = (int*)malloc(sizeof(int)*n1); 28 int *R; 29 R = (int*)malloc(sizeof(int)*n2); 30 31 int i = 0; 32 int j = 0; 33 34 for(i; i < n1; i++) 35 L[i] = array[i + p]; 36 for(j; j < n2; j++) 37 R[j] = array[j + q +1]; 38 39 i = j = 0; 40 41 int k = p; 42 43 while(i!=n1 && j!= n2) 44 { 45 if(L[i] <= R[j]) 46 array[k++] = L[i++]; 47 else 48 array[k++] = R[j++]; 49 } 50 51 while(i < n1) 52 array[k++] = L[i++]; 53 while(j < n2) 54 array[k++] = R[j++]; 55 } 56 57 void MergeSort(int array[], int p, int q) 58 { 59 if(p < q) 60 { 61 int r = (p+q)/2; 62 MergeSort(array, p, r); 63 MergeSort(array, r+1, q); 64 Merge(array,p, r, q); 65 } 66 }
参考资料:《算法导论》2.1章节
如果有什么问题,请给我留言,我会改正,我们共同进步。谢谢~